[python/파이썬] 여러 원인에 따른 결과를 분석하는 다중회귀분석

회귀분석은 원인과 결과 간의 관계를 밝혀서

원인을 통해 결과를 예측하거나 설명하는 분석방법입니다.

 

하나의 원인과

하나의 결과 간의 분석이라면,

단순회귀분석(Simple Regression Analysis)입니다.

 

여러 개의 원인과

하나의 결과 간의 분석이라면,

다중회귀분석(Multiple Regression Analysis)입니다.

 

원인과 결과 간의 관계가 

선형 관계라는 전제로 분석한다면,

선형회귀분석(Linear Regression Analysis)이며,

일반적인 회귀분석은 선형관계를 전제로 합니다. 

 

원인과 결과 간의 관계가

비선형 관계라는 전제로 분석한다면,

비선형회귀분석(Nonlinear Regression Analysis)입니다.

 

 

예제를 통해 다중회귀분석을

살펴보도록 하겠습니다.

 

통계초등학교 3학년에 재학 중인 학생 10명을 임의로 추출하여,

음식섭취량과 몸무게와 키를 쟀습니다. 

조사한 결과는 다음과 같습니다.

회귀분석은 자료를 가장 잘 설명해 주는

회귀식을 산출하고,

이를 검정하는 절차로 진행됩니다.

 

 

<다중회귀분석 1단계> 회귀식 산출

단순회귀분석의 회귀식은

Y = aX + b의 형태이나,

다중회귀분석의 회귀식은

다음과 같습니다.

원인이 되는 변수인 음식섭취량(x₁)과 몸무게(x₂)가 독립변수이고,

결과가 되는 변수인 키가 종속변수(y¡)라고 하면,

이번 다중회귀분석은 음식섭취량과 몸무게를 통해

학생의 키를 예측하는 분석입니다.

 

회귀식을 완성하기 위해서는

상수항의 회귀계수(β₀)와

음식섭취량의 회귀계수(β₁)

몸무게의 회귀계수(β₂)를 찾아내야 합니다.

 

회귀분석을 통해 찾아낸

회귀분석은 다음과 같은 형태가 됩니다. 

 

키 = 96.4860 + 0.0057음식섭취량 + 0.7129몸무게

 

최종적으로 예제의 다중회귀분석 회귀식의 회귀계수는

β₀ = 96.4860, β₁ = 0.0057, β₂ = 0.7129가 됩니다.

 

다중회귀분석의 회귀계수 구하는 식은

선형대수학을 활용하며, 다음과 같습니다.

회귀계수 β₀, β₁, β₂ = ( X' X)⁻¹ X' Y

 

회귀계수 구하는 식의 증명은 생략하나,

선형대수학 용어로 풀어보면 다음과 같습니다.

 

독립변수 X의 전치행렬(transposed matrix)과

X의 내적의 곱(dot product)을 구하고

이에 역행렬(inverse matrix)을 취한 후,

X의 전치행렬을 다시 곱하고,

독립변수 Y행렬을 곱하면,

회귀계수 β가 나옵니다.

 

파이썬을 활용하여

선형대수학을 활용한 회귀계수를 구해보겠습니다.

 

독립변수 X의 행렬을 다음과 같이 생성합니다.

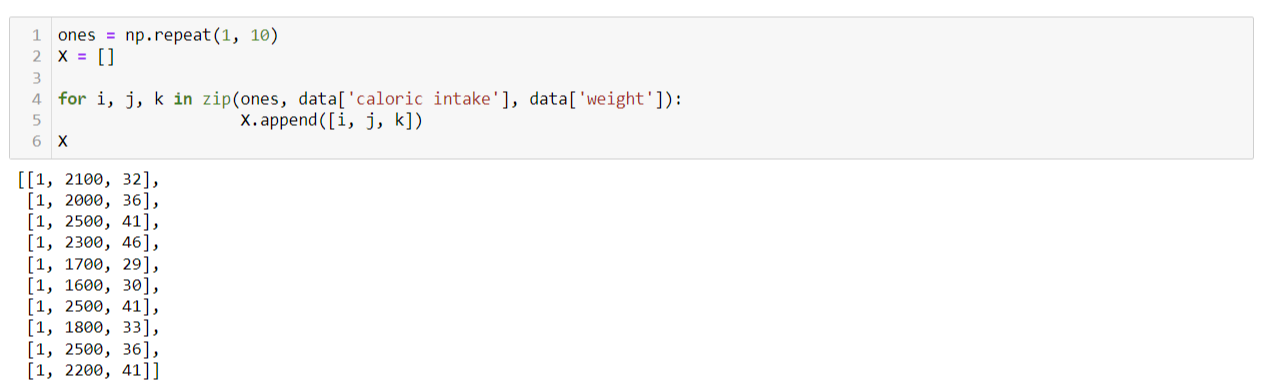
독립변수 X의 행렬에서 앞에 1이 모두 붙는 이유는.

독립변수가 곱해지지 않은 상수항 β₀를 계산하기 위해서 입니다.

 

독립변수 X의 행렬은 리스트 형태이므로,

배열(array)로 변경 후,

{자료명}.T를 활용해 전치행렬을 구합니다.

X의 전치행렬과 X행렬 간의

내적의 곱은 @를 활용합니다.

역행렬은 np.linalg.inv를 활용해서 구합니다.

여기서 linalg는 linear algebra의 줄임말이며,

inv는 inverse matrix이 줄임말입니다.

여기에 독립변수 X의 전치행렬을 다시 곱합니다.

파이썬의 과학적 표기법으로 결과가 나오며,

최종적으로 회귀계수 구하는 과정에서

일반적인 소수점으로 표기하겠습니다.

 

종속변수 Y의 행렬은 다음과 같습니다.

최종 계산결과는 다음과 같습니다.

회귀계수 β는 순서대로

β₀ = 96.486032, β₁ = 0.005658, β₂ = 0.712853이 됩니다.

 

따라서 예제의 회귀식은 다음과 같습니다.

키 = 96.486032 + 0.005658음식섭취량 + 0.712853몸무게

 

이 회귀식에 기반하여

하루 2000칼로리의 음식을 섭취하며,

몸무게가 35kg인 학생의 키를 예측하면 

다음과 같습니다

 

지금부터는 구해진 회귀식이

과연 쓸모가 있는지 검정하겠습니다.

 

 

<다중회귀분석 2단계> OLS 보고서 작성

회귀식이 유의한지 여부는

statsmodels의 OLS보고서를 활용합니다.

표본의 크기가 20보다 작아 에러가 발생하나,

이해를 돕기위한 자료이므로, 

그대로 진행합니다.

 

OLS보고서에 맞게 변형하는 방법은

다음과 같습니다.

 

우선 자료를 데이터프레임 형태가 아닌

배열(array)형태로 변경합니다.

 

구하려는 회귀식은 

상수항인 β₀가 포횜된 식이므로,

add_constant를 활용합니다.

 

OLS는 Ordinary Least Squares의 약자로서

오차의 제곱합을 최소한으로 하여,

실제값과 예측값간 차이를 최소화하기 위한 방법입니다.

 

예제의 자료를 OLS에 맞게 변경 후,

summary()를 통해 출력하면

다음과 같습니다.

OLS보고서 중 회귀분석시

주로 확인하는 사항을 살펴보겠습니다. 

종속변수	height	결정계수	0.834
모델명	OLS	수정결정계수	0.787
분석방법	최소제곱법	F검정통계량	17.62
분석일시	23년 3월 5일 일요일	F검정통계량 유의확률	0.00185
분석시각	16:56:19	로그가능도 추정량	-22.813
표본의 크기	10	아카이케 정보기준	51.63
잔차 자유도	7	베이즈 정보기준	52.53
모델(회귀) 자유도	2
공분산 유형	nonrobust

 

결정계수(R-squared)는 줄여서 R²로 표기하며 ,

0과 1사이의 범주에서  회귀식에서 관측값들을 설명하는

비율을 뜻합니다.

 

예제의 회귀식은

관측값의 83.4%를 설명합니다.

 

수정결정계수(Adj. R-squared)는

결정계수의 단점을 보완한 계수입니다.

 

단순회귀분석에서 결정계수는

회귀식의 설명력을 잘 보여주지만,

다중회귀분석에서는 독립변수의 수가 증가함에 따라

결정계수는 독립변수와 무관하게 커지는 단점이 있습니다.

따라서 이를 보완한 것이 수정결정계수입니다.

 

F검정통계량(F-statistic)은

분산분석표를 활용하여 회귀식을 검정할 때,

표본에서 산출되는 통계량을 뜻합니다.

 

확률분포인 F분포에 기반하며,

모델(회귀)자유도와 잔차의 자유도에 따라 

그래프의 개형이 달라집니다.

 

예제의 경유 모델(회귀)자유도가 2이며,

잔차의 자유도는 7이므로,

자유도 2와 7을 따르는 F분포의 개형은

다음과 같습니다.

 

F분포에서 검은색으로 얇게 표시된 부분은,

유의수준을 5%로 설정시

가설을 기각하는 영역을 보여줍니다.

 

기각하는 영역이 시작되는 지점을

기각치라고 하며 다음과 같습니다.

예제의 F검정통계량은 17.62이므로,

유의수준을 0.185%(F검정통계량 유의확률)로 설정해도

기각하는 영역에 포함됩니다.

 

F분포에 대해서는

다음 글을 참조 부탁드립니다.

https://gilber.tistory.com/43

[python/파이썬] F분포

 

다중회귀분석과 관련한 F검정통계량은

다음 글을 참조 부탁드립니다.

https://gilber.tistory.com/62

[python/파이썬] 하나의 원인에 따른 결과를 분석하는 단순회귀분석

 

AIC(아카이케 정보기준)과  BIC(베이즈 정보기준)은 

여러 회귀식(회귀모형)을 비교할 때 사용되는 값입니다.

 

다중회귀분석시 예제와는 달리

독립변수의 수가 많은 경우에 

회귀모형의 설명력은 올라가지만, 

회귀식의 적용에 어려움이 있으며,

과적합 가능성도 올라갑니다. 

 

AIC와 BIC 모두 독립변수의 수가 증가하여,

복잡한 모형이 될 수록 높은 값을 가집니다. 

따라서 동일한 설명력을 지닌 모형이라도

AIC와 BIC의 값이 낮는 모형이 더 효율적인 모형입니다.

 

AIC는 표본의 크기와는 상관없는 지표이며,

BIC는 표본의 크기가 커질 수록 높은 값을 가지므로,

많은 비용을 들여 표본의 수가 많아졌음에도 불구하고,

표본의 크기가 작은 모형과 동일한 설명력을 보여준다면

좋은 모형이라고 할 수 없습니다.

 

 

이번에는 회귀계수(coef)를 검정하겠습니다.

	회귀계수	표준오차	t검정통계량	유의확률	[0.025	0.975]
상수항	96.4860	6.482	14.885	0.000	81.158	111.814
첫번째 독립변수	0.0057	0.004	1.308	0.232	-0.005	0.016
두번째 독립변수	0.7129	0.262	2.722	0.030	0.094	1.332

 

OLS에서 회귀계수는

coef를 통해 확인합니다. 

 

회귀계수 중 constant는 상수항을,

x1은 음식섭취량을,

x2는 몸무게를 뜻하며,

앞서 구한 회귀식과 동일합니다.

 

y = 96.4860 + 0.0057(x1) + 0.7129(x2)

키 = 96.4860 + 0.0057음식섭취량 + 0.7129몸무게

 

독립변수 중에서

회귀계수가 클 수록

결과값에 더 많은 영향을 미치므로,

첫번째 독립변수보다

두번째 독립변수가 더 중요한 변수라는 사실을

확인할 수 있습니다.

 

표준오차(std err)는 추정된 회귀식과

실제 관측값 사이의 거리를 나타내지만,

자료의 크기에 따라 표준오차는 변하므로, 

회귀식을 검정할 때는 자주 사용되지 않습니다.

 

t검정통계량(t)은

회귀계수가 의미있는지 여부를 판단하는 주요 통계량이나,

회귀계수를 검정할 시에는 t검정통계량을 반영한

유의확률(P>|t|)을 확인합니다.

 

유의확률은 회귀계수가 의미가 없다는

귀무가설에 대한 확률이므로,

높을 수록 해당 회귀계수의 중요성은 떨어집니다.

 

일반적으로 유의수준을 5%(0.05)로 판단하므로,

첫번째 독립변수는 0.05보다 큰 수치로서,

해당 회귀계수로서 의미가 없습니다.

즉, 음식섭취량의 회귀계수는

통계적으로 의미가 없습니다. 

 

반면 두번째 독립변수는 0.05보다 작은 수치로서,

해당 회귀계수는 유의미한 계수이며,

따라서 몸무게의 회귀계수는

통계적으로 의미가 있습니다.

 

따라서 통계적으로 무의미한 독립변수인

음식섭취량을 제외하고,

통계적으로 유의미한 독립변수인

몸무게만을 가지고 회귀식을 만들면

다음과 같습니다.

회귀식의 설명력은 0.834에서 0.794로 떨어졌으나,

회귀식은 '키 = 98.9044 +  0.9752몸무게'로 보다 간결해졌습니다.

 

예제에서는 독립변수가 2개여서 설명력을 떨어뜨리면서까지

독립변수의 수를 줄일 필요성은 없어 보이나,

독립변수의 수가 지나치게 많은 경우에는

회귀식의 설명력은 떨어지지 않으면서도,

불필요한 독립변수를 삭제하여,

보다 효과적인 회귀식을 찾는 노력이 중요합니다.

 

 

<다중회귀분석 3단계> 다중공선성 유무 확인

마지막으로 앞선 OLS보고서의 두번째 유의사항을 보면,

해당 자료가 강한 다중공선성(Multicollinearity)이 있다는 것을

암시하고 있습니다.

다중공선성은 독립변수간에 연관성이 높은 상태를 말하며,

실제 설명력이 높은 독립변수이나,

다중공선성이 높으면 설명력이 낮은 것처럼 나타납니다.

 

독립변수들 간의 상관계수가 0.9 이상이면,

다중공선성이 있다고 판단합니다.

 

예제의 경우 음식섭취량과 몸무게 간의 상관계수는

다음과 같습니다.

상관계수가 0.9 미만이므로,

본 예제에서는 다중공선성이 없다고 판단됩니다.

 

예제의 회귀식은

통계적으로 유의미한 회귀식입니다.