카이제곱분포, t분포, F분포는
모두 일정한 규칙에 따라 검정을 하기 위한 확률분포입니다.
통계적 가설을 검정하고, 검증된 가설은
통계적으로 유의미한 가설이 되며, 진리에 다가가기 위한 열쇠가 됩니다.
카이제곱분포는 표본분산을 통해 주로 모분산을 검정하며,
t분포는 표본평균을 통해 모평균을 검정하며,
F분포는 카이제곱분포를 통해 각 집단 표본분산의 비율을 검정합니다.
일반적으로 분산의 비율을 검정하는 이유는 세가지가 있습니다.
첫째. 비교하고자하는 두 집단이 평균은 유사하나,
분산이 상이한 경우 두 집단은 다르다고 판단하기 위한 경우입니다.
둘째. 비교하고자하는 세 집단(또는 그 이상)의 평균이 모두 같은지 파악하여,
그 집단 중 한 집단이라도 다른 집단은 없는지 판단하기 위한 경우입니다.
셋째. 분산을 변화량으로 규정하고,
두 집단의 변화하는 정도를 분산의 비율로 표현하여 검토하는 경우입니다.
F분포를 이해하기 위한 시간이므로,
첫번째 검정을 중심으로 살펴보겠습니다.
두 집단이 같은지 다른지 판단하기 위해서 분산의 비율을 살펴봅니다.
두 집단의 평균이 판이하게 다른 경우에는
굳이 통계적 방법을 이용하지 않고도,
그 차이를 분명히 알 수 있습니다.
문제가 되는 경우는 평균이 유사하여,
두 집단이 같은지 다른지 판단하기 힘든 경우이며,
이 때 분산의 비율을 활용하여 판단할 수 있습니다.
이러한 분산의 비율을 검정하기 위해서
표본분산을 통해 모분산을 검정한 카이제곱분포를 활용합니다.
카이제곱분포는 다음과 같습니다.

F분포는 표본분산의 비율을 검정하므로, 분모와 분자에 각각 카이제곱분포를 정의합니다.
다만 카이제곱분포는 자유도 n-1에 따라 분포를 달리하므로,
서로 다른 두 집단의 카이제곱분포를 비교하기 위해서는 자유도의 영향력을 상쇄할 필요가 있습니다.
따라서 카이제곱분포의 정의식에서 자유도 n-1을 나눠줍니다.
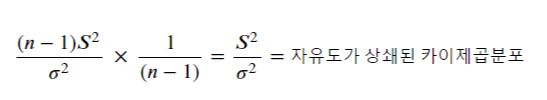
F분포의 정의식에는 분모와 분자에 각 집단의 카이제곱분포가 들어가게 됩니다.
각 집단의 표본분산과 모분산을 다음과 같이 구분짓도록 하겠습니다.


우리는 지금 두 집단의 같은지 다른지 보기위해 검정을 하고 있습니다.
그 판단기준은 모분산이며,
두 집단이 같은 집단이라면 모분산은 같다고 가정합니다.
따라서 그러한 가정에서 F의 통계량은 표본분산만을 비교합니다.

학습을 위해 통계초등학교 2학년 학생의 키에 대한 자료를 생성하겠습니다.
정규분포를 따르며, 평균이 130cm이고 표준편차가 20cm(분산은 400)인 자료를 7개씩 추출하여,
1000개의 표본을 생성하였습니다.

표본을 1000개나 생성한 이유는,
생성된 표본수가 작은 경우에는 생성된 표본의 분산과
우리가 의도한 분산인 400이 다를 수 있기 때문입니다.
통계초등학교의 모분산은 다음과 같습니다.

통계초등학교의 표본분산은 다음과 같습니다.

모분산은 각 표본들의 크기인 7로 나눠주지만,
표본분산은 표본들의 크기에서 1을 빼준 6으로 나눠구합니다.
표본분산을 구하기 위해서는,
분산을 구하는 np.var에서 ddof의 값에 1을 입력합니다.
ddof는 delta degree of freedom의 약자이며,
이는 통계학에서 자유도를 뜻하는 degree of freedom에서 나왔습니다.
delta가 붙은 이유는
delta는 두 값의 차이를 의미하기 때문입니다.
즉, 표본의 크기(여기서는 7)와 표본분산을 구하기 위한 표본의 크기(6)와의
차이를 나타내기 때문에 인자명을 ddof로 정하고 있습니다
표본의 크기에서 1을 빼주는 이유는
'카이제곱분포로 가는 표본분산 분포의 평균'을 참조 부탁드립니다.
두 집단의 비교를 위해 이번에는 확률초등학교 2학년 학생의 키에 대한 자료를 생성하겠습니다.
정규분포를 따르며, 평균이 130cm이고 표준편차가 10cm(분산은 100)인 자료를 8개씩 추출하여,
1000개의 표본을 생성하였습니다.

확률초등학교의 모분산은 다음과 같습니다.

확률초등학교의 표본분산은 다음과 같습니다.

두 초등학교의 평균과 표본분산을 한번에 비교하면 다음과 같으며,
결론적으로 평균은 유사하나, 표본분산이 다른 집단입니다.


두 초등학교가 같은지 다른지 비교하기 위한 기준을 설정하겠습니다.
우선 표본분산의 비율을 활용하여 판단할 예정이므로,
그에 합당한 F분포를 정하고,
표본분산의 비율이 F분포의 95%에 해당하는 곳에 위치한다면,
두 집단은 같은 집단이라고 판단하겠습니다.
통계초등학교에서는 자료를 7개씩 추출하였으므로, 자유도는 6이며,
확률초등학교에서는 자료를 8개씩 추출하였으므로, 자유도는 7입니다.
두 집단의 표본분산은
첫번째 자유도가 6이고, 두번째 자유도가 7인
F분포를 따르게 됩니다.

F분포는 확률분포로서 그래프에서의 면적이 곧 확률을 뜻합니다.
F분포는 두 자유도에 따라 그래프의 개형이 달라지지만,
표본의 크기 30미만에서는 오른쪽으로 꼬리가 긴 그래프를 그리게 되며,
확률을 뜻하는 면적의 상당부분이 왼쪽에 위치하고 있습니다.
따라서 F분포를 t분포와 같이
양 극단에 해당하는 경우에 한하여 확률적으로 일반적이지 않다고 판단하면 다음과 같습니다.

오른쪽 2.5%에 해당하는 값들은 일어날 확률이 희박합니다.
그러나 왼쪽 2.5%에 해당하는 값들은 일어날 확률이 희박하지 않습니다.
따라서 F분포에서는 양 극단을 판단기준으로 사용하지 않고,
오른쪽 끝만을 판단기준으로 사용합니다.
이를 F분포에 적용해보도록 하겠습니다.
두 집단 표본분산의 비율(F통계량)이 95%에 해당하는 부분에 들어오면,
애초에 가정한 두 집단이 95%의 확률로 같다고 볼 수 있으며,
나머지 5%에 해당하는 부분에 들어가면,
두 집단은 다르다고 볼 수 있습니다.

그렇다면 95%에 해당하는 두 집단 표본분산의 비율은 어느 정도일까요?
첫번째 표본의 자유도가 6이며, 두번째 표본의 자유도가 7인 F분포에서
95%에 해당하는 값은 다음과 같습니다.

통계초등학교와 확률초등학교의 표본분산의 비율은 다음과 같습니다.

애초에 두 초등학교의 모분산이 같다는 가정 하에,
표본분산의 비율이 약 3.8659보다 작으면
두 초등학교는 같은 집단이라고 결론내릴 수 있었습니다.
그러나 두 초등학교의 표본분산의 비율은 약 3.9786으로서,
통계적으로 희박한 확률에 해당하는 곳에 위치하고 있으므로,
두 초등학교는 같은 집단이 아니라고 결론내릴 수 있습니다.
학습을 위해 두 초등학교의 모분산이 다르다는 것을 알고있는 상태에서 비교하였으나,
모분산의 정보없이 표본의 자료와 F분포만 활용했을 때도
같은 결론에 도달할 수 있었습니다.
이번 비교에서는
표본분산의 비율이 0에서부터 95%에 해당하는 값 사이에 들어오는 경우에 두 집단이 같다고 판단하고,
95%의 값이 넘어가는 경우에는 두 집단이 다르다고 판단하였습니다.
그렇다면, 우리의 판단기준을 어느 정도로 해야, 두 집단을 같다고 판단할 수 있을까요?
두 집단의 표본분산의 비율은 다음과 같았습니다.

F분포 그래프의 개형을 결정하는 pdf(probability density function)는 다음과 같습니다.
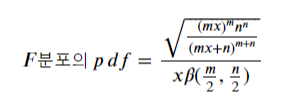
이를 활용하여, 0부터 두 표본분산의 비율까지의 면적(확률)을 구하겠습니다.
면적을 구하기 위해 적분이 필요하며, 이를 위해 sympy를 활용합니다.
파이썬은 영어소문자 x와 변수로서 x를 구분하지 못하므로,
sympy.symbols을 통해 변수 x를 규정하고,
F분포의 식에서 적분값을 구하면 다음과 같습니다.

수식에 직접 대입하여 해결하였으나,
pdf의 면적은 cdf(cumulative distribution function)을 활용하면,
0에서부터 해당 값까지의 면적을 구할 수 있으며, 결과는 동일합니다.

그래프로 표현하면 다음과 같습니다.

우리가 판단기준을 95.329%로 했다면,
두 초등학교가 같다고 결론지을 수도 있었습니다.
하지만 우리가 궁금한 것은
두 집단의 표본분산의 비율을 감안했을 때,
두 집단이 같을 확률입니다.
이를 p-value라고 부릅니다.
우리가 판단기준을 95.329%까지 올려야만
두 초등학교가 같다고 결론 지을 수 있다면,
사실상 그 두 초등학교는 다르다고 보는 것이 합리적입니다.
따라서 F분포에서 p-value는
1에서 해당표본분산의 비율까지 확률을 빼서 구하며,
다음과 같습니다.

즉, 통계초등학교와 확률초등학교의 표본을 봤을 때,
두 초등학교가 같을 확률은 약 4.67% 정도이므로,
두 초등학교는 통계적으로는 다르다고 판단하게 됩니다.
F분포의 가장 기본적인 기능은
오늘 예제와 같이 집단간 표본분산의 비율을 검정하는 것이며,
사용을 확대하여 분산분석, 회귀분석에도 활용됩니다.
분산분석과 회귀분석은 다음 기회에 다루도록 하겠습니다.
'확률분포 > 연속형 확률분포' 카테고리의 다른 글
| [python/파이썬] t분포 (0) | 2023.02.09 |
|---|---|
| [python/파이썬] 카이제곱분포 (0) | 2023.02.07 |
| [python/파이썬] 카이제곱분포로 가는 표본분산 분포의 분산 (2) | 2023.02.03 |
| [python/파이썬] 카이제곱분포로 가는 표본분산 분포의 평균 (0) | 2023.02.02 |
| [python/파이썬] 카이제곱분포로 가는 표본평균 분포의 분산 (0) | 2023.02.01 |
| [python/파이썬] 카이제곱분포로 가는 표본평균 분포의 평균 (0) | 2023.01.31 |
| [python/파이썬] 카이제곱분포로 가는 모분산 (0) | 2023.01.30 |
| [python/파이썬] 카이제곱분포로 가는 모평균 (2) | 2023.01.30 |