[python/파이썬] 원인과 결과의 관계가 다차원인 다항회귀분석

회귀분석은 원인과 결과 간의 관계를 밝혀서

원인을 통해 결과를 예측하거나 설명하는 분석방법입니다.

 

원인과 결과 간의 관계가 

선형 관계라는 전제로 분석한다면,

선형회귀분석(Linear Regression Analysis)이며,

일반적인 회귀분석은 선형관계를 전제로 합니다. 

 

원인과 결과 간의 관계가

비선형 관계라는 전제로 분석한다면,

비선형회귀분석(Nonlinear Regression Analysis)입니다.

 

여기서 주의할 점은,

단순회귀분석 기준으로

회귀식이 Y = aX + b이 아니라,

회귀식이 y = ax² + b의 형태인 경우라도

선형회귀분석에 속한다는 점입니다.

 

그 이유는 회귀식 중 ax²은

x²을 X로 치환하면, 

결국 최종 회귀식은 Y = aX + b의 형태가 되기 때문입니다.

 

선형과 비선형의 관계는

자료가 분포된 형태로 구분하는 것이 아니라,

독립변수 간의 관계가 선형이라는 의미입니다.

 

다만, 일차식인 ax + b의 회귀식과

이차식인 ax² + bx + x의 회귀식을 구분하기 위해서

이차식보다 상위 다항식을 활용한 회귀분석시에는

다항회귀분석(Polynomial Regression Analysis)이라고 합니다. 

 

 

예제를 통해 다항회귀분석을

살펴보도록 하겠습니다.

 

통계초등학교 3학년에 재학 중인 학생 9명을 임의로 추출하여,

몸무게와 성적을 측정하였으며,

조사한 결과는 다음과 같습니다.

이를 산포도로 표현하면 다음과 같습니다.

이를 statsmodels의 OLS를 통해

일반적인 회귀식으로 산출하면,

다음과 같은 회귀식이 나옵니다.

y = -0.25몸무게 + 97.4444

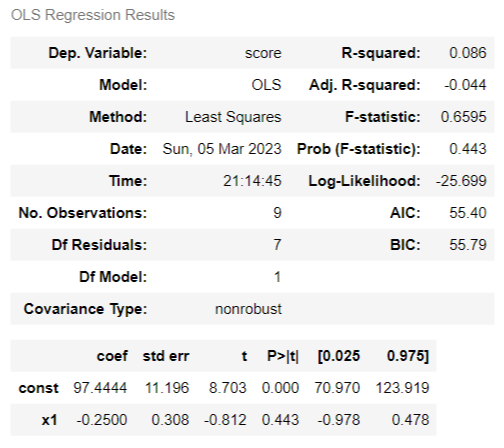
회귀식은 산출되었으나,

관측값들을 설명하는 비율인 R-squared가 0.086으로,

관측값의 8.6%밖에 설명하지 못합니다.

 

종속변수의 유의확률도 0.443으로

회귀계수가 무의미하다는 것을 알 수 있습니다.

 

OLS보고서 읽는 방법은

아래 글을 참조 부탁드립니다.

https://gilber.tistory.com/63 

[python/파이썬] 여러 원인에 따른 결과를 분석하는 다중회귀분석

 

이렇게 구한 회귀식을 산포도에 투영해도

회귀식이 잘못되었다는 사실을 알 수 있습니다.

수식을 직접 입력한 산포도를 그려도

결과는 같습니다.

이러한 경우에는 회귀식을 별도로 찾아야 합니다.

 

 

<다항회귀분석 1단계> 회귀식 산출

예제에 걸맞는 회귀식을 찾기 위해

np.polyfit을 사용합니다.

첫번째 인자는 독립변수가 들어가며,

두번째 인자는 종속변수가 들어가며,

세번째 인자는 다항식의 차수가 들어갑니다.

 

다항식의 차수가 1차식이라면,

앞선 회귀계수와 동일한 회귀계수가 산출됩니다.

다항식의 차수가 2차식이라면,

세번째 인자에 2를 입력하며,

결과는 다음과 같습니다.

회귀계수에서 차항이 높은 순으로 출력되며,

이를 반영한 식은 다음과 같습니다. 

y = -0.17911255x² + 12.6461039x -129.90909091

 

이를 산포도에 반영한 그래프는

다음과 같습니다.

 

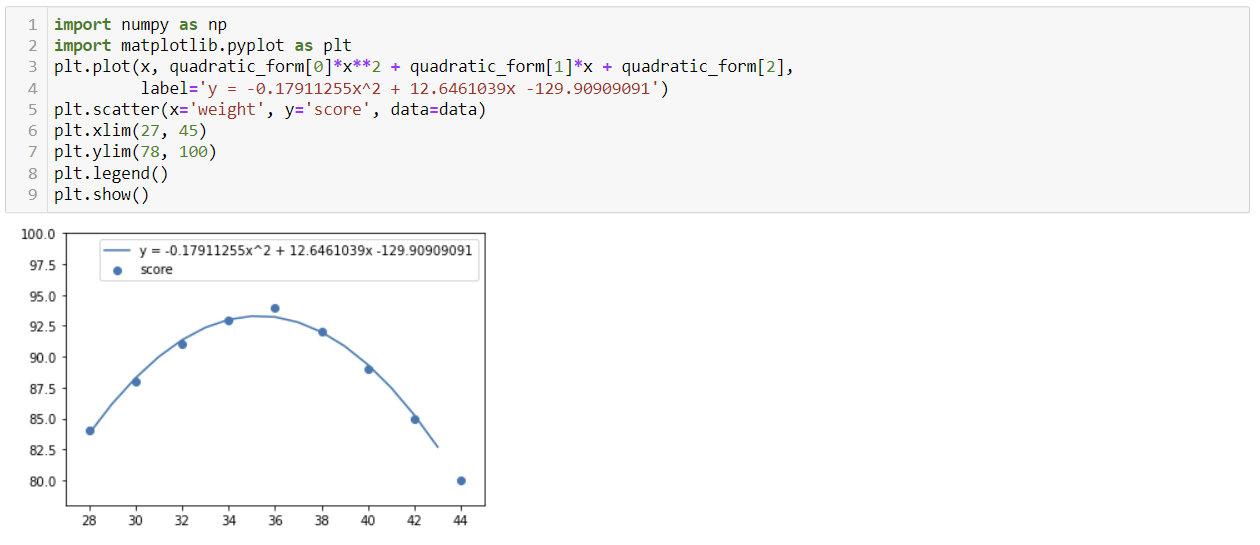
<다중회귀분석 2단계> OLS 보고서 작성

다중회귀분석 1단계를 통해

1차식에 비해 2차식이 예제 데이터에 적합하다는 것을

알게 되었습니다.

 

2차 다항회귀식이 유의한지 여부도

1차와 동일하게,

statsmodels의 OLS보고서를 활용합니다.

 

다만, 별도의 식을 입력하지 않고 OLS보고서를 작성하면,

1차식과 동일하게 출력되므로,

데이터의 현황과 동떨어진 회귀식을 기반으로 

결과물이 나옵니다. 

 

따라서 다항회귀분석의 경우에는

별도로 식을 입력해야 합니다.

 

별도의 식은 from_formula를 통해 입력합니다.

 

2차 다항식이라면

'종속변수 ~ np.square(독립변수) + 독립변수'의 식을 입력합니다.

상수항을 포함하기 위한 add_constant는 생략합니다.

표본의 크기가 20보다 작아 에러가 발생하나,

이해를 돕기위한 자료이므로, 

그대로 진행합니다.

산출된 회귀식은 다음과 같습니다.

y = -0.1791몸무게² + 12.6461몸무게 -129.9091

 

앞서 np.polyfit에서 산출된 회귀식과 동일합니다.

 

1차식의 회귀식으로는

R-squared가 0.086으로, 관측값의 8.6%밖에 설명하지 못했으나,

2차식의 회귀식으로는

R-squared가 0.994으로, 관측값의 99.4%를 설명할 수 있습니다.

 

종속변수 회귀계수 유의확률도 모두 0.05 미만이므로

산출된 회귀계수는 통계적으로 유의미한 회귀계수입니다.

 

 

3차 다항식이라면

'종속변수 ~ np.power(독립변수, 3) + np.square(독립변수) + 독립변수'의 식을 입력합니다.

상수항을 포함하기 위한 add_constant는 생략합니다.

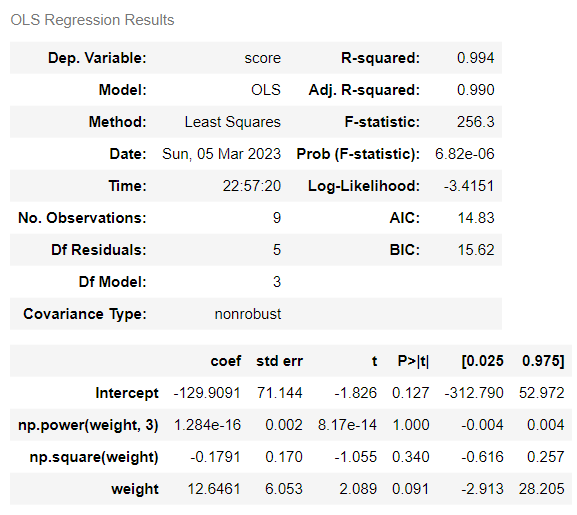
산출된 회귀식은 다음과 같습니다.

y = 0.0000000000000001284몸무게³  -0.1791몸무게² + 12.6461몸무게 -129.9091

3차 다항식의 회귀계수가 산출은 되었으나,

0에 가까운 수치이며,

앞서 2차 다항식에서 산출된 회귀식과 동일합니다.

 

1차식의 회귀식으로는

R-squared가 0.086으로, 관측값의 8.6%밖에 설명하지 못했으나,

2차식의 회귀식으로는

R-squared가 0.994으로, 관측값의 99.4%를 설명할 수 있었으며,

3차식의 회귀식으로는

R-squared가 0.994으로, 관측값의 99.4%를 설명할 수 있으나,

3차 다항식의 회귀계수가 무의미하므로.

2차 다항식의 회귀계수와 다를 바 없습니다.

 

3차 다항식의 종속변수 유의확률을 보더라도

모두 유의확률이 0.05를 넘어가므로

산출된 회귀계수는 통계적으로 무의미한 회귀계수입니다.

 

 

다항회귀분석시 주의할 점은

다음과 같습니다.

 

일반적으로 다항식의 차수를 높일 경우

관측값의 설명력이 올라 갈 수 있으나,

과적합가능성이 높습니다. 

 

5차 다항식에서는

일반 해가 없다는 사실이 아벨에 의해 증명되었으며,

실무적으로도

5차 이상의 다항회귀분석은

해석이 용이하지 않아 자주 사용되지 않습니다.