올해 통계초등학교 2학년 학생 16명의 키를 조사한 결과,
표본평균은 125cm였습니다.


정확하게 평균을 125cm에 근접한 자료를 생성하는 방법은,
아래 글을 참고 부탁드립니다.
[python/파이썬] 모분산을 알고 있는 경우 모평균 검정 예제
작년도 우리나라 2학년 학생의 키를 조사한 결과, 평균이 130cm이며, 표준편차가 12cm였습니다. 올해 통계초등학교 2학년 학생 36명의 키를 조사한 결과, 표본평균은 125cm였습니다. 정확하게 평균을
gilber.tistory.com
임의추출한 이 표본의 표본분산은 다음과 같습니다.

모분산은 각 표본들의 크기로 나눠주지만,
표본분산은 표본들의 크기에서 1을 빼준 수로 나눠 구합니다.
표본의 크기에서 1을 빼주는 이유는,
아래 글을 참고 부탁드립니다.
[python/파이썬] 카이제곱분포로 가는 표본분산 분포의 평균
카이제곱분포, t분포, F분포는 모두 일정한 규칙에 따라 검정을 하기 위한 확률분포입니다. 통계적 가설을 검정하고, 검증된 가설은 통계적으로 유의미한 가설이 되며, 진리에 다가가기 위한 열
gilber.tistory.com
표본분산을 구하기 위해서는,
분산을 구하는 np.var에서 ddof의 값에 1을 입력합니다.
ddof는 delta degree of freedom의 약자이며,
이는 통계학에서 자유도를 뜻하는 degree of freedom에서 나왔습니다.
delta가 붙은 이유는
delta는 두 값의 차이를 의미하기 때문입니다.
즉, 모분산을 구하기 위한 표본의 크기와
표본분산을 구하기 위한 표본의 크기와의
차이를 나타내기 때문에 인자명을 ddof로 정하고 있습니다
표본분산의 식은 다음과 같습니다.

수식에 직접 대입하여, 계산한 분산의 결과는
sample.var(ddof=1)의 결과와 같습니다.

우리는 우리나라 2학년 전체의 평균키를 검정하고자 합니다.
현재 우리나라 2학년 전체의 평균키는 130cm으로 추정됩니다.
여기서 우리나라 2학년은 우리가 알고자 하는 모집단입니다.
이러한 모집단의 특성을 보여주는 평균, 표준편차, 분산 등을 모수라고 합니다.
각각의 모수는 모평군, 모표준편차, 모분산이라고 부릅니다.
모수에 대해서 펼치는 주장을 가설이라고 합니다.
모수에 대해서 새로운 주장을 한다면,
기존의 주장과는 대립되므로 대립가설이라고 합니다.
만약 대립가설이 타당하지 않다면,
기존의 주장으로 돌아가게 되므로, 기존의 주장을 귀무(歸無)가설이라고 합니다.
돌아갈 귀(歸)와 없을 무(無)의 귀무이며,
돌아가서 보니 변한 건 없다는 의미입니다.
<가설검정 1단계> 귀무가설과 대립가설 설정
귀무가설은 다음과 같습니다.
우리나라 2학년 학생의 키의 평균은 130cm이다.
대립가설은 다음과 같습니다.
우리나라 2학년 학생의 키의 평균은 130cm가 아니다.
이제는 새로운 주장인 대립가설이 맞는지 확인할 통계 수단을 찾아야 합니다.
우리는 통계초등학교 2학년의 표본만 살펴볼 예정이므로,
단일표본입니다.
우리는 우리나라 2학년 학생의 평균 및 모분산을 모릅니다.
통계초등학교 2학년 학생의 표본수는 16이므로,
소표본에 해당됩니다.
<가설검정 2단계> 검정통계량 설정
표본이 단일표본이고 소표본이며,
모분산을 모르므로,
t 통계량을 사용하기로 합니다.
이를 가설을 검정할 때 사용하는 통계량이므로,
검정통계량이라고 합니다.
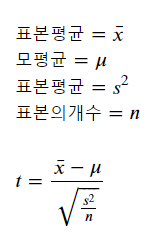
소표본에 사용되는 t분포는,
아래 글을 참조 부탁드립니다.
[python/파이썬] t분포
카이제곱분포, t분포, F분포는 모두 일정한 규칙에 따라 검정을 하기 위한 확률분포입니다. 통계적 가설을 검정하고, 검증된 가설은 통계적으로 유의미한 가설이 되며, 진리에 다가가기 위한 열
gilber.tistory.com
우리는 가설이 타당한지 여부를 결정해 줄 검정통계량으로
t분포를 정했습니다.
t분포는 그래프의 면적이 확률을 나타내는 확률분포이며,
그래프의 개형은 다음과 같습니다.
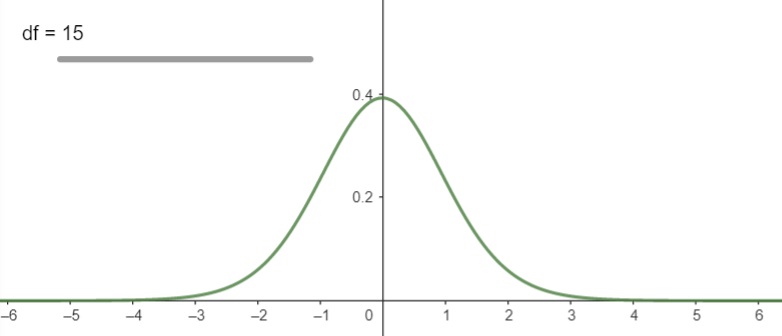
t분포는 평균이 0인 좌우대칭이며,
기준인 0을 중심으로 +1, -1 사이에 많은 자료값들이 분포가 되어있습니다.
t분포는 정규분포와 유사하지만,
정규분포와는 다른 대표적인 비정규분포입니다.
그래프 아래의 면적이 곧 확률이므로,
기준에서 멀어질수록 확률은 줄어들게 됩니다.
일반적으로는 발생할 확률이 5%도 채 되지 않는다면,
통계적으로는 발생할 확률이 없다고 판단합니다.
그리고 좌우대칭인 t분포에서 보면,
양 극단에 2.5% 내의 확률로 발생하는 사건도,
통계적으로는 발생할 확률이 없다고 판단합니다.
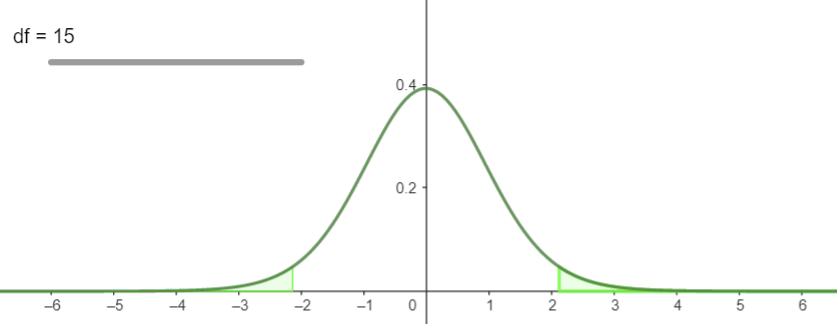
양 극단의 2.5%에 해당하는 t통계량 값은 다음과 같습니다.
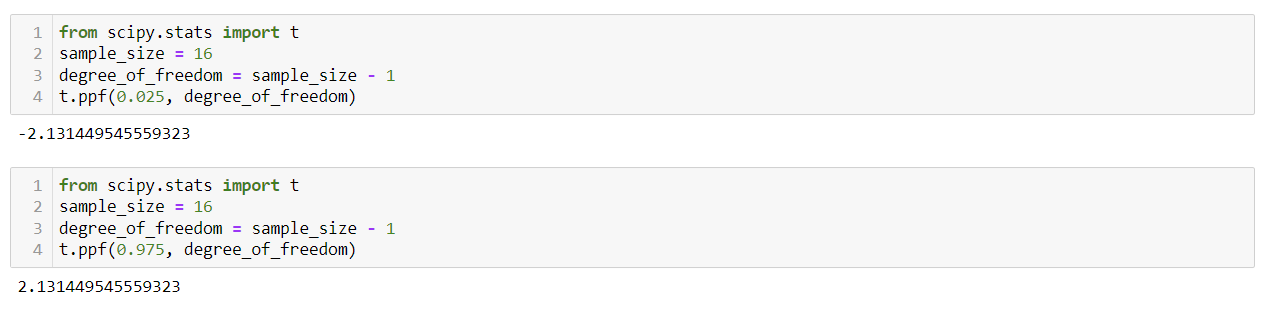
왼쪽 기준으로 2.5%인 곳과 97.5%인 곳의 값을 기준으로 하게 되며,
좌우대칭인 t분포이므로, 각각의 값은 부호를 달리할 뿐 같습니다.
실제 모든 소수점을 표기하기 번거로우므로,
보통 +/- 2.13으로 표기합니다.
<가설검정 3단계> 유의수준 설정
우리는 발생할 확률이 5%도 채 되지 않는다면,
가설을 받아들이지 않기로 하였습니다.
이때 기준이 되는 확률이 바로 유의수준입니다.
유의수준은 보통 %로 표시하지 않고,
소수점으로 표현하므로
5% 대신 0.05로 표기합니다.
다만, 양 극단에 해당하는 경우,
모두 발생할 확률이 희박하다는 의미이므로,
0.05를 반으로 나눠서 양 극단에서 0.025 떨어진 곳에 해당하는 경우에
기존가설(귀무가설)을 받아들이지 않기로 하겠습니다.
우리는 현재 작년의 평균을 믿어도 괜찮은지 판단하는 중이며,
작년의 평균을 기준으로 발생할 확률을 살펴보았으나,
발생확률이 5%로도 되지 않는 경우라면,
기존가설을 받아들이지 않는 것이 타당하기 때문입니다.
즉 우리가 기준으로 삼은 검정통계량이
-2.131449545559323 보다 적거나,
2.131449545559323 보다 많은 경우에는
기존 귀무가설을 받아들이지 않기로 하겠습니다.
<가설검정 4단계> 검정통계량 계산
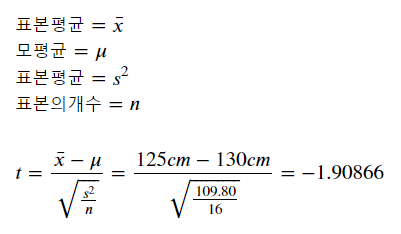
이번 예제의 검정통계량 값은 약 -1.90866입니다.
직접 수식에 대입하여 얻은 결과는 다음과 같습니다.

scipy의 단일표본인 t통계량을 구하는
ttest_1samp를 활용해도 결과는 같습니다.
일부 소수점 차이는 있으나,
직접 대입하는 과정에서 입력된 소수점의 차이이며,
같은 방식으로 계산된 결과입니다.

<가설검정 5단계> 통계적 판단
우리는 기준으로 삼은 검정통계량이
-2.131449545559323 보다 적거나,
2.131449545559323 보다 많은 경우에는
기존가설(귀무가설)을 받아들이지 않기로 하였습니다.
검정통계량이 −1.90866284848393이므로,
-2.131449545559323 보다 크고,
2.131449545559323 보다 작기 때문에
우리나라 2학년 학생들의 키의 평균이 130cm이라는
기존 주장을 채택하게 됩니다.
이를 통계적인 표현으로는
귀무가설을 채택한다고 표현합니다.
가설의 기각여부는 귀무가설을 중심으로 표현하지만,
결론은 대립가설을 기준으로 표현합니다.
따라서 이번 예제의 결론은 다음과 같습니다.
유의수준 5%에서 검정결과,
우리나라 2학년 학생의 키의 평균은 130cm가 아니라는 대립가설을
기각합니다.
'가설검정 > 모평균 가설검정' 카테고리의 다른 글
| [python/파이썬] 대응표본에서 모평균 차이 검정 예제 (0) | 2023.02.24 |
|---|---|
| [python/파이썬] 소표본에서 두 모분산은 모르지만 모분산이 다를 경우 두 모평균 차이 검정 예제 (0) | 2023.02.17 |
| [python/파이썬] 소표본에서 두 모분산은 모르지만 모분산이 같을 경우 두 모평균 차이 검정 예제 (0) | 2023.02.15 |
| [python/파이썬] 대표본에서 두 모분산을 모르는 경우 두 모평균 차이 검정 예제 (0) | 2023.02.15 |
| [python/파이썬] 대표본에서 두 모분산을 아는 경우 두 모평균 차이 검정 예제 (0) | 2023.02.15 |
| [python/파이썬] 모분산을 아는 경우 모평균 검정 예제 (0) | 2023.02.13 |