카이제곱분포, t분포, F분포는
모두 일정한 규칙에 따라 검정을 하기 위한 확률분포입니다.
통계적 가설을 검정하고, 검증된 가설은
통계적으로 유의미한 가설이 되며, 진리에 다가가기 위한 열쇠가 됩니다.
이중 카이제곱분포는 t분포와 F분포의 기반이 되는 분포입니다.
카이제곱분포로 가는 시리즈는 다음과 같이 구성됩니다.
1. 카이제곱분포로 가는 모평균
2. 카이제곱분포로 가는 모분산
3. 카이제곱분포로 가는 표본평균 분포의 평균
4. 카이제곱분포로 가는 표본평균 분포의 분산
5. 카이제곱분포로 가는 표본분산 분포의 평균
6. 카이제곱분포로 가는 표본분산 분포의 분산
7. 카이제곱분포
오늘은 카이제곱분포로 가는 표본평균 분포의 분산에 대해서입니다.
표본평균 분포의 평균은 모평균을 추종하는 각각의 표본으로 인해 모평균이 됩니다.
그렇다면 표본평균 분포의 분산은 모분산이 된다고 생각할 수 있으나,
모분산보다 적은 값이 됩니다.
분산은 자료가 분포된 정도입니다.
모집단은 표본에 비해 자료의 분포된 정도가 훨씬 넓습니다.
그리고 표본의 평균이 이루는 분포의 분산은 훨씬 더 구간이 좁은 구간에 분포하게 됩니다.
표본은 모집단의 일부를 추출한 결과이므로 그러합니다.
그렇다면 표본의 평균이 이루는 분포의 분산은 모분산에 비해 얼마나 좁은 구간에 분포하게 될까요?
당연히 모분산과 연관성은 쉽게 추측할 수 있습니다.
그 외의 중요한 요소로서 표본의 개수를 생각해 볼 수 있으나, 표본의 개수는 답이 아닙니다.
각 표본마다 몇 개의 값을 추출했는지가 표본평균 분포의 정도를 결정하게 됩니다.
기존과 동일하게 통계초등학교의 키에 대한 자료를 생성하겠습니다.
정규분포를 따르며, 평균이 130cm이고 표준편차가 10cm인 자료를 10개씩 추출하여,
10000개의 표본을 생성하였습니다.

생성된 첫번째 표본을 살펴보겠습니다.

10개의 자료값이 있으며, 평균은 대략 137.38cm입니다.
우리는 지금 표본으로 뽑은 자료의 평균이 분포하는 정도를 파악하고자 합니다.
10000개의 표본평균을 다 열거할 수 없으나,
처음 일부만 열거하면 다음과 같습니다.

seaborn을 활용하여, 표본평균의 분포를 그려보겠습니다.

정규분포에 근사한 분포가 확인됩니다.
우리가 알고자했던 이 표본평균 분포의 분산은 다음과 같습니다.

예제는 평균 130cm, 표준편차가 10cm인 자료를 10개씩 추출하여 생성된 10000개의 표본이었습니다.
모분산이 100(표준편차 10의 제곱)인 자료에서,
표본평균 분포의 분산은 대략 10(표본평균 분포의 분산 9.64)이 나왔습니다.
결국 각 표본평균이 이루는 분포의 분산은,
모분산을 각 표본마다 추출한 자료의 개수로 나눈 값입니다.
예제를 바꾸어서 표본평균의 분산을 구해보도록 하겠습니다.
아까와 동일한 조건이나, 이번에는 자료를 20개씩 추출하겠습니다.

표본마다 추출한 갯수를 2배로 늘렸더니, 표본평균 분포의 분산은 절반이 되었습니다.


표본마다 추출한 갯수를 3배로 늘렸더니, 표본평균 분포의 분산은 1/3이 되었습니다.

수학적으로는 다음과 같습니다.




각 표본평균이 이루는 분포의 분산은
모분산(𝜎²)을 각 표본마다 추출한 자료의 개수(n)로 나눈 값입니다.
결론은 나왔으나,
증명과정 중 직관적이지 않은 다음 부분만 별도로 증명하도록 하겠습니다.
분산에 관한 식에서 상수 1/n이 대괄호 밖으로 나오면서 제곱으로 나오는 부분입니다.

분산을 정리하기 위해서는 평균이 정리되어 있어야 합니다.
편차란 자료 안의 각각의 값에서 평균을 빼고난 값을 뜻하며,
분산은 편차의 제곱을 합한 후 자료의 갯수로 나눈 것을 뜻하기 때문입니다.
X₁의 평균을 알고 있는 상태에서 aX₁+b의 평균은 a(X₁의 평균)+b가 됩니다.
예를 들면 표본을 몇개 뽑아서 평균을 냈더니 3이었다면,
이 표본 각각의 값에 4를 곱하고 5를 더한 값의 평균은 4 x 3 + 5가 되어 17이 됩니다.
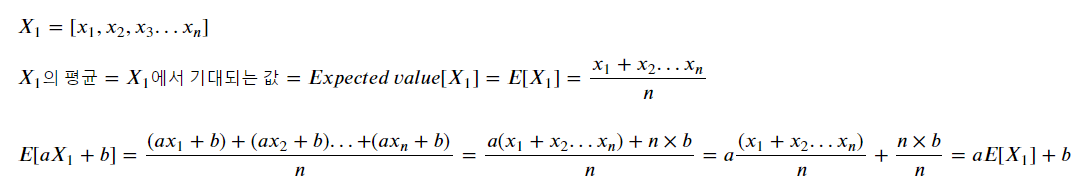
분산에 관한 식도 이와 유사합니다.
X₁의 분산을 알고 있는 상태에서 aX₁의 분산은 상수 a²(X₁의 분산)이 됩니다.
예를 들면 표본을 몇개 뽑아서 분산을 구했더니 3이었다면,
이 표본 각각의 값에 2를 곱한 값의 분산은 2² × 3이 되어 12가 됩니다.
분산의 식에 곱해진 상수a가 분산의 식 밖으로 나올 때 제곱이 되어 나오는 이유는 다음과 같습니다.

정리하면,
모집단에서 표본을 n개씩 뽑아서 평균을 낸 것을 표본평균이라고 하며,
이러한 표본평균이 이루는 분포를 표본평균의 분포라고 합니다.
표본평균의 분포의 평균은 모집단의 평균인 모평균과 같으며,
표본평균의 분포의 분산은 모집단의 분산인 모분산이 아니라,
모분산을 각 표본을 뽑은 개수인 n개로 나눈 값과 같습니다.
지금까지는 표본평균을 다뤘으며, 다음시간에는 표본분산을 다룹니다.
카이제곱분포는 모분산이 특정값을 갖는지 검정하기 위한 분포이므로,
표본분산에 대한 이해는 카이제곱분포를 이해하기 위해 필요한 부분입니다.
다음은 카이제곱분포로 가는 표본분산의 분포의 평균입니다.
'확률분포 > 연속형 확률분포' 카테고리의 다른 글
| [python/파이썬] t분포 (0) | 2023.02.09 |
|---|---|
| [python/파이썬] 카이제곱분포 (0) | 2023.02.07 |
| [python/파이썬] 카이제곱분포로 가는 표본분산 분포의 분산 (2) | 2023.02.03 |
| [python/파이썬] 카이제곱분포로 가는 표본분산 분포의 평균 (0) | 2023.02.02 |
| [python/파이썬] 카이제곱분포로 가는 표본평균 분포의 평균 (0) | 2023.01.31 |
| [python/파이썬] 카이제곱분포로 가는 모분산 (0) | 2023.01.30 |
| [python/파이썬] 카이제곱분포로 가는 모평균 (2) | 2023.01.30 |
| [python/파이썬] 감마분포 (0) | 2023.01.21 |