카이제곱분포, t분포, F분포는
모두 일정한 규칙에 따라 검정을 하기 위한 확률분포입니다.
통계적 가설을 검정하고, 검증된 가설은
통계적으로 유의미한 가설이 되며, 진리에 다가가기 위한 열쇠가 됩니다.
이중 카이제곱분포는 t분포와 F분포의 기반이 되는 분포입니다.
카이제곱분포로 가는 시리즈는 다음과 같이 구성됩니다.
1. 카이제곱분포로 가는 모평균
2. 카이제곱분포로 가는 모분산
3. 카이제곱분포로 가는 표본평균 분포의 평균
4. 카이제곱분포로 가는 표본평균 분포의 분산
5. 카이제곱분포로 가는 표본분산 분포의 평균
6. 카이제곱분포로 가는 표본분산 분포의 분산
7. 카이제곱분포
오늘은 카이제곱분포로 가는 표본평균 분포의 평균에 대해서입니다.
우리가 알고자하는 집단을 모집단이라고 하며,
일반적으로 우리는 모집단 전체의 자료를 갖기가 불가능합니다.
따라서 모평균을 구할 수 없습니다.
다만 모집단의 특성은 표본(샘플)을 통해 가늠해 볼 수 있습니다.
즉 일정한 샘플을 뽑아서 평균을 구하여 추정합니다.
그렇지만 한번의 샘플을 통해 전체 모집단을 추정하는 것은 매우 어렵기 때문에,
샘플을 최대한 뽑아 평균을 낸 후, 이를 다시 돌려놓고,
다시 샘플을 최대한 뽑아 평균을 낸 후, 이를 다시 돌려놓는 작업을 반복합니다.
이를 복원추출이라고 합니다.
카이제곱분포는 복원추출을 기반으로 구성됩니다.
복원추출을 바탕으로 표본의 평균을 측정하면,
매 추출시마다 표본평균은 달라지게 됩니다.
그리고 매번 다른 표본평균은 분포를 이루게 되며,
이 분포의 평균이 바로 표본평균 분포의 평균입니다.
즉 매 표본마다의 평균은 우리가 알고자 하는 모평균과 다르지만,
표본평균 분포의 평균은 우리가 알고자하는 모평균과 같습니다.
정말 그럴까요?
첫 번째 표본과 두 번째 표본을 10개씩 뽑았더니 다음의 결과가 나왔습니다.

복원추출을 가정하였으므로, 같은 값들이 반복해서 나올 수도 있습니다.
앞선 시리즈에서 통계초등학교 2학년 4반 학생들의 키와 같이
평균키가 130cm이고 표준편차가 10cm인 자료를 생성하겠습니다.
1.76405235e+00과 같은 과학적 표기법보다, 직관적으로 이해하기 쉽도록
numpy의 set_printoptions를 지정하였습니다.
precision을 활용하여 소수 몇째 자리까지 표기할지 정할 수 있으며,
suppress를 True로 설정하면 과학적 표기법을 해제할 수 있습니다.
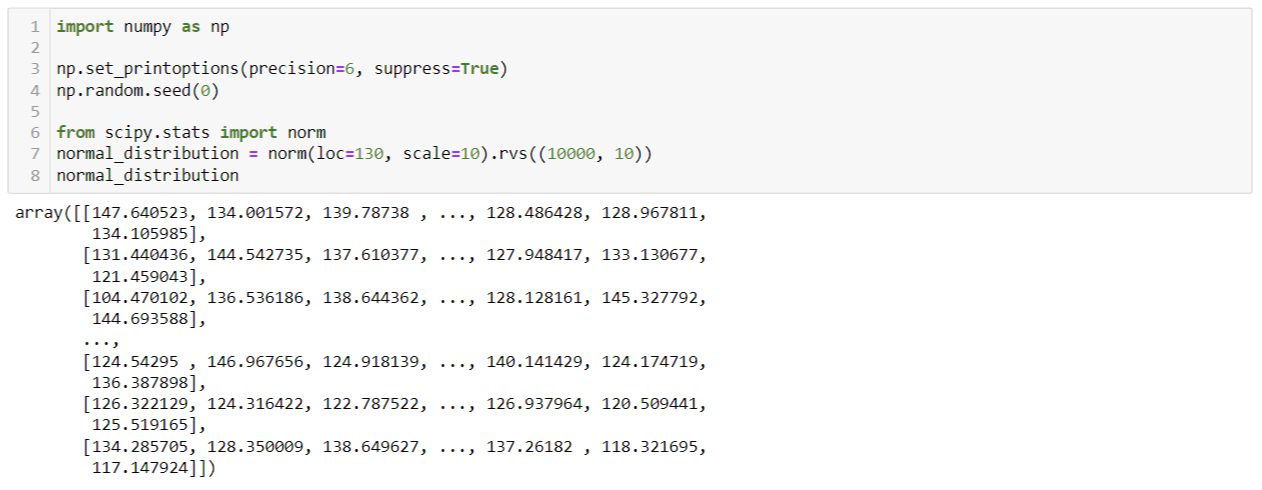
정규분포를 따르며, 평균이 130cm이고 표준편차가 10cm인 자료를 10개씩 추출하여,
10000개의 데이터를 생성하였습니다.
첫 번째 표본을 살펴보겠습니다.

자료는 생성되었으나, 첫번째 표본의 평균은 137.38cm으로 우리가 가정한 평균 130cm과 차이가 있습니다.
두 번째 표본을 살펴보겠습니다.

자료는 생성되었으나, 두번째 표본의 평균은 134.00cm으로 여전히 우리가 가정한 평균과 차이가 있습니다.
이처럼 평균과 차이가 있는 표본평균을 분포로 만들어 평균을 내면 정말 모평균이 나오는지 확인해 보겠습니다.
생성된 표본 10000개 각각의 평균을 보겠습니다.

전체를 표기할 수는 없으나, 앞서 확인한 첫 번째, 두 번째 표본은 확인되었습니다.
이 표본들의 평균은 다음과 같습니다.

우리가 가정한 평균 130cm과 정확하기 일치하지는 않지만, 상당히 유사함을 확인할 수 있습니다.
즉 10개씩 표본(샘플)을 뽑아서 나온 각각의 평균은 모평균과 일치하지 않지만,
이러한 표본평균들의 평균은 모평균과 일치하게 됩니다.
수학적으로는 다음과 같습니다.
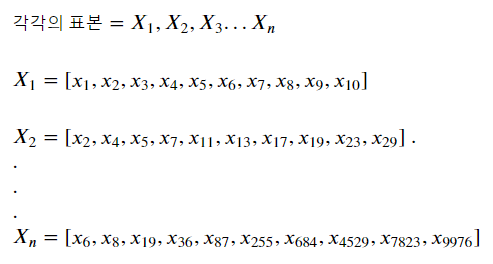



표본평균 분포의 평균은 모평균을 추종하는 각각의 표본으로 인하여,
결국 모평균이 됩니다.
당연한 결론이라고 생각될 수 있으나,
앞으로 다룰 표본평균분포의 분산은 우리의 직관과 어긋나는 부분이 있습니다.
카이제곱분포는 모분산이 특정값을 갖는지 검정하기 위한 분포이므로,
표본분산에 대한 이해는 카이제곱분포를 이해하기 위해 필요한 부분입니다.
다음은 카이제곱분포로 가는 표본평균의 분포의 분산입니다.
'확률분포 > 연속형 확률분포' 카테고리의 다른 글
| [python/파이썬] 카이제곱분포 (0) | 2023.02.07 |
|---|---|
| [python/파이썬] 카이제곱분포로 가는 표본분산 분포의 분산 (2) | 2023.02.03 |
| [python/파이썬] 카이제곱분포로 가는 표본분산 분포의 평균 (0) | 2023.02.02 |
| [python/파이썬] 카이제곱분포로 가는 표본평균 분포의 분산 (0) | 2023.02.01 |
| [python/파이썬] 카이제곱분포로 가는 모분산 (0) | 2023.01.30 |
| [python/파이썬] 카이제곱분포로 가는 모평균 (2) | 2023.01.30 |
| [python/파이썬] 감마분포 (0) | 2023.01.21 |
| [python/파이썬] 지수분포 (0) | 2023.01.18 |