통계는 변수를 다루는 학문입니다.
원주율을 의미하는 π나, 자연상수를 의미하는 e와 같은 상수는 변하지 않는 수로서 의의를 지니지만,
통계의 본질은 변하는 수를 이해하고, 예측하는 데 있습니다.
변수는 랜덤하게 발생하거나, 일정한 확률을 가지고 발생합니다.
일정한 확률을 바탕으로 발생하는 변수를 확률변수(Random Variable)라고 합니다.
주사위의 눈은 1, 2, 3, 4, 5, 6만 가능하며, 1.54와 같은 수는 나오지 않습니다.
이처럼 가능한 값들이 이산가족과 같이 흩어져 있는 확률변수가 이산확률변수입니다.
수학적으로 이산확률변수는 모든 원소들이 정수와 일대일로 대응하는 변수를 의미합니다.
주사위와는 달리 키와 몸무게와 같이 연속적으로 변하는 값들도 있습니다.
키의 자료값이 170센티미터, 180센티미터와 같이 떨어져 있는 것으로 보이지만,
실제 데이터에 들어갈 수 있는 자료는 170.000001도 가능하며,
연속적으로 어떤 수치도 들어갈 수 있는 확률변수를 연속확률변수라고 합니다.
연속확률변수(Continuous Random Variable)
연속확률변수는 음의 무한대부터 양의 무한대까지 정의될 수 있습니다.
'정의될 수 있다'고 표현한 이유는,
확률변수의 특성에 따라 변수의 범위가 달라지게 되기 때문입니다.
예를 들어 키는 음의 값이 나올 수 없으며,
상황에 따라 키의 조건을 지정하고 범위를 구할 수도 있기 때문입니다.
이산확률변수와는 달리 연속확률변수는 각각의 변수가 하나의 확률에 대응할 수 없습니다.
예를 들어 누군가의 키가 170센티미터일 확률을 구한다면,
170.000001센티미터일 확률, 170.000002센티미터의 확률 등으로 구할 수 있어야 하나 불가능합니다.
그래서 연속확률변수의 확률은 구간으로 구합니다.
예를 들어 누군가의 키가 165센티미터 이상 175센티미터 이하일 확률로 구합니다.
연속확률변수를 만들어 보겠습니다.
연구결과, 연속확률변수는 0과 2 사이에서만 발생하며,
수식은 다음과 같다고 알게 되었다고 가정하겠습니다.
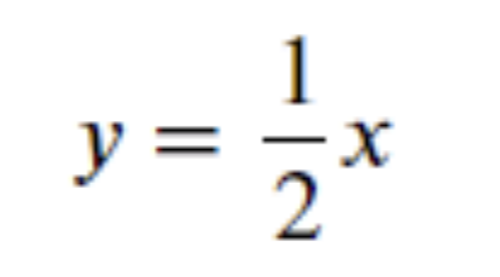
대략적인 그래프를 보기 위해 0과 2사이에 0.05 간격으로 점을 찍을 준비를 합니다.

matplolib.pyplot을 활용하여 그래프를 그립니다.
plot은 그린다는 뜻입니다.
첫번째 인수인 x는 계산할 점들이며, 두번째 인수는 사용할 수식입니다.

적분계산을 위해 sympy를 가져옵니다.

파이썬은 문자인 'x'와 변수의 'x'를 구분하지 못하므로,
symbols를 통해 x가 변수라고 알려줍니다.
integrate는 적분하는 메서드이며,
첫번째 인수는 적분할 수식을 입력하고,
두번째 인수는 괄호 안에 변수, 적분을 시작하는 점, 적분을 끝내는 점을 입력합니다.
결과는 1입니다.
연속확률변수는 수식의 그래프 아래의 면적이 확률을 의미하며,
구간 내의 모든 확률을 더한 결과는 1이 됩니다.
우리가 알고자 하는 것은 변수가 1.5와 2 사이 일 때의 확률입니다.
계산결과는 다음과 같습니다. 즉 43.75%입니다.

위의 데이터의 연속확률변수에 대해서, 확률에 기반하여 기대되는 값(기댓값)을 구하겠습니다.
기댓값은 연속확률변수의 각 값들(x)과 이에 해당하는 수식인 f(x)를 곱하고 표현된 식의 면적입니다.

참고로 아래는 이산확률변수의 기댓값이며, 시그마 대신에 인테그랄을 사용한 점이 다를 뿐,
각각의 값들과 해당하는 확률을 곱한 후 모두 더한다는 의미에서 본질적으로 같은 식입니다.

기댓값은 다음과 같습니다.

기댓값의 수식과 같이, 변수(x)와 연구결과와 얻어진 수식(x/2)을 곱하고, 이를 적분(integrate)하여 구합니다.
기댓값이 나왔으나, 기댓값만으로 이 데이터를 충분히 설명한다고 보기 어려우므로,
기댓값을 중심으로 자료값들이 흩어진 정도를 파악해 볼 필요가 있으며,
분산을 활용합니다.
분산은 편차를 활용하며,
편차는 각각의 확률변수에서 기댓값을 뺀 것을 뜻합니다.
분산은 각각의 편차를 제곱하고, 각각에 해당하는 확률을 곱한 후, 모두 더한 값입니다.

분산을 구하기 위해 다음을 입력합니다.

표준편차는 분산의 제곱근이므로 다음과 같습니다.
제곱근은 numpy의 sqrt로 구합니다.

참고로 float은 데이터값을 실수로 바꿔주는 명령어이며,
variance를 그대로 입력하면, 에러가 발생합니다.
variance는 2/9가 아닌 sympy.integrate((x-expected_value)**2 * x/2, (x, 0, 2)이기 때문입니다.
그래서 이를 유한한 값으로 바꿔준 후 제곱근을 구해야 합니다.
위 데이터에서 확률에 기반하여 기대되는 값은 4/3로서 대략 1.3333이며,
기댓값에서 표준편차를 뺀 값인 0.8619(1.3333 - 0.4714)와,
기댓값에서 표준편차를 더한 값인 1.8047(1.3333 + 0.4714) 사이에서
상당수의 자료값이 분포되어 있다는 결론이 나옵니다.
수식에 기반하여 직접적으로 계산하였으나,
일반적으로는 식을 유도하여 다음의 공식을 더 자주 활용합니다.

유도된 식에 기반하여 분산을 계산하면 다음과 같습니다.
각각의 연속확률변수를 제곱한 기대값을 구하고, 기댓값의 제곱을 빼줍니다.
결과는 원래의 식으로 계산한 결과와 동일합니다.

연속확률변수의 기댓값과 분산에 기반하여 연속형 확률분포가 나옵니다.
연속형 확률분포에는
균등분포, 정규분포, 표준정규분포, 지수분포, 감마분포, 카이제곱분포, F분포, t분포 등이 있습니다.
데이터가 특정 연속형 확률분포를 따른다면,
해당 데이터의 특성을 보다 명확히 이해하고, 통계에 근거한 예측을 할 수 있습니다.
'기초통계 > 확률변수' 카테고리의 다른 글
| [python/파이썬] 이산확률변수 (1) | 2023.01.04 |
|---|