변수는 랜덤 하게 발생하거나, 일정한 확률을 가지고 발생합니다.
일정한 확률을 바탕으로 발생하는 변수를 확률변수(Random Variable)라고 합니다.
확률변수들이 모여 확률분포를 이루게 됩니다.
데이터의 확률분포를 알고 있다면,
일어날 수 있는 사건의 확률을 알 수 있고, 확률에 근거한 판단을 내릴 수 있습니다.
확률분포는 주사위처럼 결괏값이 떨어져 있는 이산형 확률분포와
키와 몸무게와 같이 연속적으로 변하는 값들로 이뤄진 연속형 확률분포가 있습니다.
이산형 확률분포에는
베르누이 시행, 이항분포, 포아송분포, 기하분포, 음이항분포, 초기하분포 등이 있습니다.
연속형 확률분포에는
균등분포, 정규분포, 표준정규분포, 지수분포, 감마분포, 카이제곱분포, F분포, t분포 등이 있습니다.
초기하분포( Hypergeometric Distribution)
초기하분포는 일반적으로 품질관리를 위해 사용됩니다.
전수검사를 통해 모든 제품을 확인하면 비용과 시간이 과도하게 소모되어
제조단가가 치솟게 되고, 이는 경쟁력저하로 이어지게 됩니다.
따라서 과거의 자료를 통해 전체 상품 중에 불량품의 평균적인 비율을 알고 있을 때,
임의로 선택한 상품이 불량품일 확률을 추측하고, 이에 대응하기 위해 초기하분포를 활용합니다.
과거자료를 통해 5개의 상품 중 1개가 불량품이었다는 사실이 알려져 있습니다.
5개 상품을 모두 검사하기 불가하여, 2개의 상품을 샘플로 검사하기로 하였습니다.
2개의 상품을 샘플로 검사하였을 때, 1개의 상품이 불량품일 확률을 구해보겠습니다.
확률은 해당 사건수를 전체 경우의 수입니다.
5개의 상품 a, b, c, d, e 중에서 2개의 상품을 검사하는 전체 경우의 수는 10가지입니다.
(a, b) // (a, c) // (a, d) // (a,e) // (b, c) // (b, d) // (b, e) // (c, d) // (c, e) // (d, e)

5개의 상품 중 1개가 불량품이고, 상품 b가 불량이라고 가정하겠습니다.
모든 경우의 수에서 b가 포함된 경우는 (a, b) // (b, c) // (b, d) // (b, e)가 있으며,
총 4가지 경우의 수가 있습니다.
따라서 2개를 뽑았을 때,
그 중 한 개가 불량품일 확률은 40%(해당 사건수 4 / 전체 경우의 수 10)입니다.
우리가 기존에 5개 중 1개가 불량이라는 정보를 바탕으로,
2개의 상품을 검수하였을 때 40%의 확률로 그 중 1개가 불량품이라는 사실을 알았습니다.
초기하분포의 식은 다음과 같습니다.
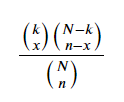
N은 총 상품의 수이며, 예제에서는 5입니다.
k는 과거 자료를 통해 알 수 있는 사실로서, 총 상품 중에서 불량품의 수이며, 예제에서는 1입니다.
따라서 N - k는 과거 자료를 통해 알 수 있는 사실로서, 총 상품중에서 양품의 수이며, 4가 됩니다.
n은 이번에 확인하고자 하는 샘플의 수이며, 예제에서는 2가 됩니다.
x는 샘플 중에서 불량품의 수이며, 예제에서는 1이 됩니다.
초기하분포는 궁극적으로 n개 중에서 x개가 불량품일 확률을 구하는 분포이며,
샘플로 뽑힌 상품은 검수 후에 다시 집어넣지 않는 비복원추출입니다.
이 식의 의미는 다음과 같습니다.
우선 확률을 구하는 식이므로, 분모에는 전체 경우의 수가 나옵니다.
예제에서 5개 중에서 2개를 뽑는 경우의 수 10가지 입니다.


초기하분포식의 분자는 우리가 알고 있는 정보를 바탕으로 합니다.
과거 자료를 통해 기존 상품의 수(N)에서 불량품의 수(k)와 양품의 수(N-k)를 알고 있으며,
그 불량품(k) 중에서 이번에는 몇 개의 불량품(x)이 나올 지 경우의 수를 구하고,
그 양품(N-k) 중에서 이번에는 몇개의 양품(n-x)이 나올지 경우의 수를 구하여 곱합니다.
다시 예제로 돌아가겠습니다.
과거자료를 통해 5개의 상품 중 1개가 불량품이었다는 사실이 알려져 있습니다.
5개 상품을 모두 검사하기 불가하여, 2개의 상품을 샘플로 검사하기로 하였습니다.
2개의 상품을 샘플로 검사하였을 때, 1개의 상품이 불량품일 확률을 구해보겠습니다.
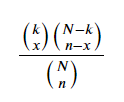


수식을 이해하기 위해 직접 구하였으나,
scipy의 hypergeom.pmf를 이용하여 간단히 구할 수도 있습니다.
pmf는 probability mass function의 약자로서,
지금처럼 사건의 발생 횟수라는 띄엄띄엄 있는 결괏값들을 구할 때,
특정 값에 대한 확률을 나타내는 함수를 뜻합니다.
hypergeom.pmf의 첫 번째 인자는 우리가 알고자 하는 샘플 중의 불량품 수이며,
두 번째 인자는 총 상품 수이며,
세 번째 인자는 기존 알려진 불량품 수이며,
네 번째 인자는 이번에 뽑는 샘플 수입니다.

이번에는 같은 자료이나,
2개의 상품을 샘플로 검사하였을 때, 1개의 상품이 불량품일 확률이 아니라,
1개 이하의 상품이 불량품일 확률을 구하겠습니다.
즉 불량품이 1개가 나오거나, 불량품이 나오지 않는 경우의 확률을 더하도록 하겠습니다.
이는 scipy의 hypergeom.cdf를 이용하여 간단히 구할 수도 있습니다.
cdf는 cumulative distribution function의 약자로서,
1개 이하의 상품이 불량품일 누적 확률을 구합니다.

결괏값은 1, 즉 100%가 나왔습니다.
이는 2개의 샘플을 뽑았을 때, 불량품이 전혀 나오지 확률과 불량품이 1개가 나올 확률의 합과 같습니다.

2개의 샘플을 뽑았으므로, 2개 모두 불량품일 확률도 있으므로, 100%가 나온 것이 의외일 수 있습니다.
이는 문제의 가정이 5개의 상품 중 1개의 상품만 불량품이라는 사실 하에 정의되었기 때문입니다.
전체 상품에서 1개의 상품이 불량인데, 2개를 뽑는다고 해서 2개의 불량품이 나오지는 않기 때문입니다.
초기하분포의 기댓값을 구하겠습니다.
즉, 총 N개의 상품 중에서 k개의 불량품이 있는데,
n개의 상품을 뽑으면, 불량품은 몇 개 나올지에 관해서입니다.
초기하분포의 기댓값은 다음과 같습니다.


이는 2개의 샘플을 뽑았을 때, 0.4개의 불량품이 나올 것으로 기대된다는 의미입니다.
hypergeom.expect의 메서드를 이용해도 결과는 동일합니다.

초기하분포의 분산을 구해보도록 하겠습니다.
즉, 기댓값을 통해 어느 정도 도전해야 성공하는지 파악은 하였으나,
그 결괏값을 신뢰할 수 있는 범주는 어느 정도인지 파악할 수 있습니다.
초기하분포의 분산은 다음과 같습니다.

예제에 대입하면 결과는 다음과 같습니다.

hypergeom.var의 메서드를 이용해도 결과는 동일합니다.

분산은 편차를 제곱한 값이므로, 데이터의 퍼진 정도가 제곱이 되어 있습니다.
이를 원래의 수준으로 되돌리기 위해서, 통상적으로 루트를 씌워서 제곱근을 구합니다.
하지만 분산이 1 미만인 경우에는 제곱근을 통해 분산이 확대되므로, 분산을 그대로 활용합니다.
이를 활용하여 평균적으로 기대되는 불량품 수는 다음과 같습니다.

즉, 5개의 상품 중 1개의 불량품이 있는 경우에,
2개의 샘플을 뽑았을 때, 불량품은 평균적으로 최소 0.16개가 나오거나,
평균적으로 최대 0.64개가 나올 확률이 높습니다.
초기하분포는 이항분포와 달리 표본분포를 돌려놓지 않는 비복원추출입니다.
다만 초기하분포의 상품수(N)가 충분히 큰 경우는 이항분포로 근사하여 계산합니다.
'확률분포 > 이산형 확률분포' 카테고리의 다른 글
| [python/파이썬] 음이항분포 (0) | 2023.01.13 |
|---|---|
| [python/파이썬] 기하분포 (1) | 2023.01.10 |
| [python/파이썬] 포아송분포 (1) | 2023.01.10 |
| [python/파이썬] 이항분포 (0) | 2023.01.07 |
| [python/파이썬] 베르누이 시행 (0) | 2023.01.06 |