[python/파이썬] 균등분포(균일분포)

변수는 랜덤 하게 발생하거나, 일정한 확률을 가지고 발생합니다.

일정한 확률을 바탕으로 발생하는 변수를 확률변수(Random Variable)라고 합니다.

 

확률변수들이 모여 확률분포를 이루게 됩니다.

 

데이터의 확률분포를 알고 있다면, 

일어날 수 있는 사건의 확률을 알 수 있고, 확률에 근거한 판단을 내릴 수 있습니다. 

 

확률분포는 주사위처럼 결괏값이 떨어져 있는 이산형 확률분포와

키와 몸무게와 같이 연속적으로 변하는 값들로 이뤄진 연속형 확률분포가 있습니다.

 

이산형 확률분포에는

베르누이 시행, 이항분포, 포아송분포, 기하분포, 음이항분포, 초기하분포 등이 있습니다.

 

연속형 확률분포에는

균등분포,  정규분포, 표준정규분포, 지수분포, 감마분포, 카이제곱분포, F분포, t분포 등이 있습니다.

 

 

균등분포(Uniform Distribution)

특정 구간에서 확률을 바탕으로 발생하는 확률변수가 모두 같다고 한다면, 

즉 균등하게 분포되어 있다면, 이는 해당 구간에 한하여 균등분포를 따른다고 합니다.

 

특정 구간에서 발생하는 사건만을 다루기 때문에,

특정 구간 이외의 나머지 구간에서의 확률은 모두 0이 됩니다.

 

예를 들어, 사건이 발생하는 구간은 1부터 5 사이이며, 

해당 구간내의 모든 확률값은 0.25로 균일하다고 가정하겠습니다.

그래프로 나타내면 다음과 같습니다. 

연속형 확률분포에서 모든 면적의 합은 1이 되어야 합니다.

균등분포의 경우 모든 확률값이 같으므로, 그래프 개형은 직사각형이 되고,

가로인 구간의 길이(1과 5 사이)와 확률값 0.25의 곱은 1이 됩니다. 

따라서 확률값 0.25는 우연히 정해진 값이 아니며, 

구간의 길이가 4라면, 균일분포의 확률값은 반드시 1/4 즉 0.25가 되어야만 합니다. 

 

구간 a와 b 사이에서 균일분포의 식은 다음과 같습니다.

a와 b 사이의 거리를 구하기 위해 b에서 a를 빼고, 

이를 역수를 취하여, 두 수의 곱이 1이 되는 식이 됩니다.

 

예제의 균일분포 식은 다음과 같습니다. 

즉 예제의 균일분포에서 확률변수에 따른 확률은 모두 0.25로 같습니다.

 

scipy의 uniform.pdf를 활용해도 결과는 같습니다. 

uniform은 균등분포(uniform distribution)를 뜻합니다.

pdf는 확률밀도함수(probability density function)를 뜻하며,

확률변수에 따른 확률값을 알려줍니다.

구간 밖에서는 모든 확률이 0이며, 

구간 내에서는 모든 확률이 균등합니다.

 

여기서 uniform.pdf의 첫번째 인자는 x에 확률변수 값을 입력하며, 

loc는 균등분포의 구간 시작점을 입력하며, 

scale은 균등분포의 구간 시작점에서 떨어진 거리를 입력합니다. 

 

즉 uniform.pdf(x=2, loc=1, scale=4)는

1에서 시작하고, 5(loc + scale)까지 구간을 가지는 균등분포에서, 

확률변수가 2일 때 해당하는 확률을 알려주게 됩니다.

 

그렇다면, 1.6에서 3.2사이의 구간에 대한 확률은 어떻게 구할까요?

연속형 확률변수는 구간사이의 면적이 확률이며, 

그래프의 면적은 적분을 통해 구합니다.

 

적분계산을 위해 sympy를 가져옵니다.

파이썬은 문자인 'x'와 변수의 'x'를 구분하지 못하므로,

symbols를 통해 x가 변수라고 알려줍니다. 

integrate는 적분하는 메서드이며, 

첫 번째 인수는 적분할 수식을 입력하고,

두 번째 인수는 괄호 안에 변수, 적분을 시작하는 점, 적분을 끝내는 점을 입력합니다.

 

1.6과 3.2 사이 구간의 면적은 0.4입니다.

연속확률변수는 그래프 아래의 면적이 확률을 의미하며, 

구간 내의 모든 확률을 더한 결과는 1이 됩니다. 

 

이해를 돕기 위해 적분을 사용하였으나,

scipy의 uniform.cdf를 활용하여 같은 결과를 얻을 수 있습니다. 

uniform은 균등분포(uniform distribution)를 뜻합니다.

cdf는 누적분포함수(cumulative density function)를 뜻하며,

균일분포의 가장 왼쪽 끝에서부터 특정 지점까지의 면적, 즉 확률을 알려줍니다. 

 

우리가 알고자 하는 구간은 1.6과 3.2사이이므로, 

가장 왼쪽 끝에서부터 3.2까지의 확률에서, 

가장 왼쪽 끝에서부터 1.6까지의 확률을 빼서, 우리가 알고자 하는 확률을 알 수 있습니다.

 

 

균일분포의 기댓값은 다음과 같습니다.

예제는 균등분포를 따르는 사건이 1부터 5까지 발생하는 경우이며, 

이 경우 기댓값은 다음과 같습니다. 

이 균등분포에서 평균적으로 기대되는 값은 3입니다. 

바로 균등분포에서 중앙값입니다. 

 

식을 이해하기 위해 직접 대입하였으나,

scipy의 uniform.expect를 활용해도 결과는 동일합니다. 

 

균등분포의 분산은 다음과 같습니다. 

예제를 적용하면 다음과 같습니다.

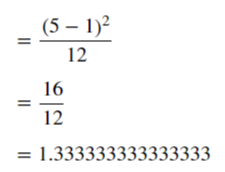
수식을 이해하기 위해 직접 대입하였으나, 

scipy의 uniform.var를 이용해도 결과는 동일합니다.

 

여기서 균등분포는 연속형 균등분포로 정의하였으나,

주사위와 같이 모든 눈의 확률이 동일한 경우처럼, 이산형 균등분포에서도 정의됩니다. 

 

균등분포는 확률변수에 따른 특정 확률을 지정할 수 없는 경우,

구간 내에 모든 확률이 동일하다는 가정을 통해 확률을 구하고자 할 때 사용합니다.