[python/파이썬] 기하분포

변수는 랜덤하게 발생하거나, 일정한 확률을 가지고 발생합니다.

일정한 확률을 바탕으로 발생하는 변수를 확률변수(Random Variable)라고 합니다.

 

확률변수들이 모여 확률분포를 이루게 됩니다.

 

데이터의 확률분포를 알고 있다면, 

일어날 수 있는 사건의 확률을 알 수 있고, 확률에 근거한 판단을 내릴 수 있습니다. 

 

확률분포는 주사위처럼 결괏값이 떨어져 있는 이산형 확률분포와

키와 몸무게와 같이 연속적으로 변하는 값들로 이뤄진 연속형 확률분포가 있습니다.

 

이산형 확률분포에는

베르누이 시행, 이항분포, 포아송분포, 기하분포, 음이항분포, 초기하분포 등이 있습니다.

 

연속형 확률분포에는

균등분포,  정규분포, 표준정규분포, 지수분포, 감마분포, 카이제곱분포, F분포, t분포 등이 있습니다.

 

 

기하분포(Geometric Distribution)

결괏값이 성공과 실패, 합격과 불합격, 앞면과 뒷면 등과 같이,

단 두 가지의 가능성만 있을 때 이를 베르누이 시행이라고 합니다. 

베르누이 시행은 한 번의 시행을 전제로 하며, 

이러한 베르누이 시행을 반복적으로 행한 결과,

처음 성공할 때까지 시행 횟수에 따른 확률은 기하분포를 따릅니다.

이 식이 의미하는 바는 다음과 같습니다.

만약 세 번째 성공한다면, 첫 번째와 두 번째는 실패해야만 합니다. 

그래서 첫 번째 실패할 확률 x 두 번째 실패할 확률 x 세 번째 성공할 확률로 나타나며,

성공확률은 처음 성공하는 단 한번의 성공만을 필요로 하므로 한 번만 곱합니다.

실패확률은 성공하기 직전까지 실패할 확률이므로 시행횟수에서 1을 차감한 수만큼

제곱하여 곱해줍니다. 

 

 

연구 결과, 어떤 사건이 성공할 확률은 0.7 즉 70%라고 가정하겠습니다.

따라서 실패할 확률은 1에서 성공할 확률 0.7을 뺀 0.3이며, 30%입니다. 

이 사건이 한 번 발생하면 베르누이 시행과 동일하며,

실패 없이, 바로 성공할 확률을 구해보겠습니다. 

수식을 이해하기 위해 직접 구하였으나,

scipy의 geom.pmf를 이용하여 간단히 구할 수도 있습니다.

pmf는 probability mass function의 약자로서, 

지금처럼 사건의 발생 횟수라는 띄엄띄엄 있는 결괏값들을 구할 때,

특정 값에 대한 확률을 나타내는 함수를 뜻합니다.

geom.pmf의 첫 번째 인자는 기준이 되는 시행 횟수이며,

두 번째 인자에는 성공확률을 입력합니다.

한 번의 실패 후, 두 번째 성공할 확률을 구해보겠습니다.

두 번의 실패 후, 세 번째 성공할 확률을 구해보겠습니다.

세번 안에 성공할 확률을 구해보겠습니다. 

한 번에 성공할 수도 있으며, 두 번째에 성공할 수도 있으며, 세 번째에 성공할 수도 있습니다.

이 모든 경우의 수를 포함하는 확률을 구해보겠습니다.

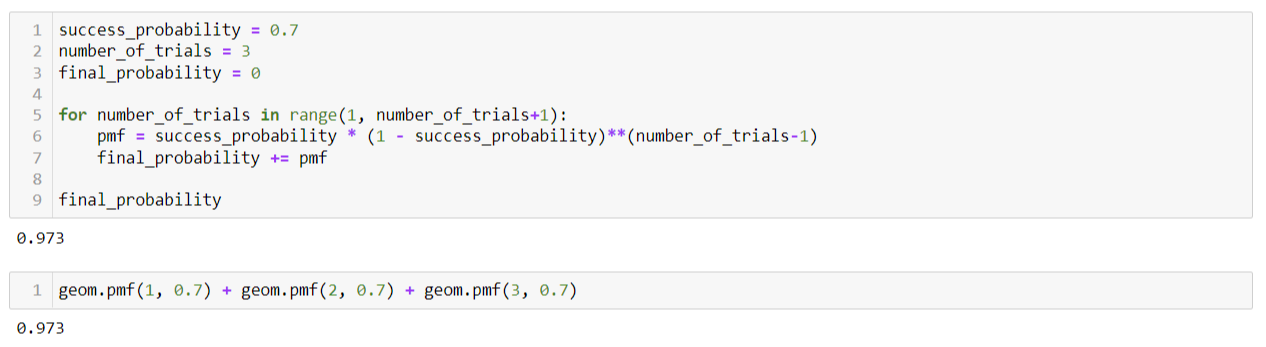
수식에 이해하기 위해 직접 계산하여 확률을 구하였으나,

scipy의 geom.cdf를 이용하여 간단히 구할 수도 있습니다.

cdf는 cumulative distribution function의 약자로서, 

세 번 안에 성공할 확률을 예로 들면, 

첫 번째, 두번째, 세번째까지의 확률을 누적하여 보여주는 함수입니다.

 

geom.cdf의 첫번째 인자는 기준이 되는 시행 횟수이며,

두 번째 인자에는 성공확률을 입력합니다.

이는 성공확률이 70%로 상당히 높은 경우이므로,

세 번의 시행 안에 성공할 확률이 97.3%로 높게 나타납니다.

 

만약 성공확률이 5%로 상당히 낮은 경우에는

세번의 시행을 하더라도 성공할 확률이 14.26%로 낮게 나타납니다.

 

기하분포의 기댓값을 구하겠습니다. 

즉, 평균적으로 어느 정도 도전해야 성공할 수 있는지에 대해서입니다.

 

성공확률을 p라고 할 때, 기하분포의 기댓값은 다음과 같습니다.

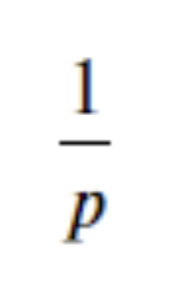
이 기댓값은 기하분포 식에서 출발합니다.

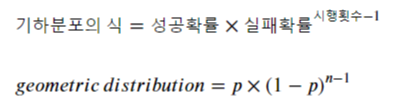
기댓값은 첫번째 시행결과 + 두번째 시행결과 + 세번째 시행결과 + ... 무한의 시행결과의 합입니다.

무한의 시행을 가정하는 이유는 언제 성공할지 모르는 상태에서, 무한번 실패할 수도 있기 때문입니다. 

 

기하분포도 이산확률변수의 하나로서,

이산확률변수의 기대값과 같이 각 변수와 해당 변수의 확률을 곱한 값들을 모두 합하여 구합니다. 

우선 i와 관련이 없는 p를 시그마 밖으로 빼냅니다.

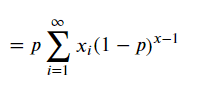
시그마 내부의 형태를 보면 (1-p)의 x승을 (1-p)에 대해 미분한 것과 같습니다.

 

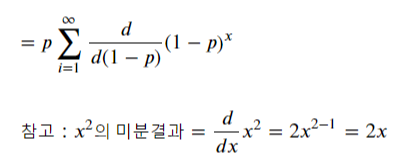
미분한 식도 시그마 밖으로 꺼냅니다.

무한등비수열은 첫번째 항에서 계속 같은 수를 곱하여 나온 수열입니다.

그 같은 수를 공평하게 비례하게 한다는 의미에서 공비라고 합니다.

첫째항을 a, 공비를 r로 하는 수열은 다음과 같습니다. 

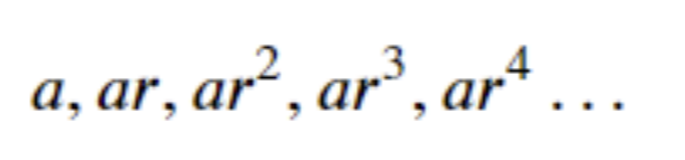
이러한 수열이 무한정 계속되는 경우 무한등비수열이라고 하며,

공비가 1보다 작은 무한등비수열을 모두 합하면 그 합은 다음과 같습니다.

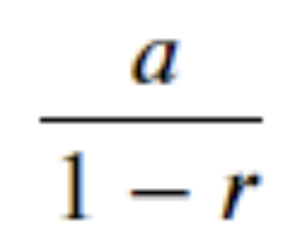
기하분포의 (1-p)의 x승도 무한등비수열입니다.

 

식을 정리하면 다음과 같습니다.

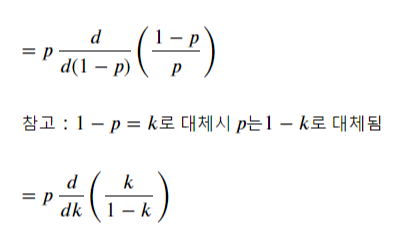
결과적으로  (1-p)에 대한 미분식이 k에 대한 미분식으로 변경되었습니다.

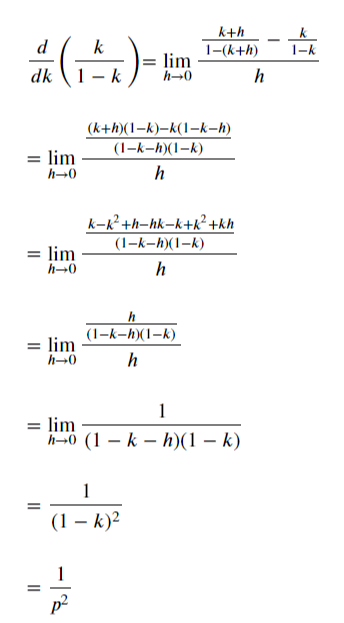
기존 정리된 수식은 다음과 같습니다.

미분결과를 적용하면 다음과 같이 되며,

기하분포의 기댓값이 도출됩니다.

 

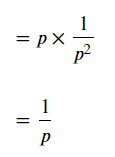
성공확률이 70%인 경우 기댓값은 다음과 같습니다.

평균적으로 1.43번은 도전해야 성공을 기대할 수 있습니다.

geom의 메서드를 활용해도 결과는 동일합니다.

 

기하분포의 분산을 구하겠습니다.

즉, 기댓값을 통해 어느 정도 도전해야 성공하는지 파악은 하였으나,

그 결괏값을 신뢰할 수 있는 범주는 어느 정도인지 파악할 수 있습니다.

 

기하분포의 분산은 다음과 같습니다.

 

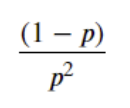
성공확률이 70%인 경우 분산은 다음과 같습니다.

geom의 메서드를 활용해도 결과는 동일합니다

분산은 편차를 제곱한 값이므로, 데이터의 퍼진 정도가 제곱이 되어 있습니다.

이를 원래의 수준으로 되돌리기 위해, 루트를 씌워서 제곱근을 구합니다. 

이렇게 구해진 값을 표준편차라고 하며, numpy의 sqrt를 이용합니다.

 

이를 활용하여 평균적으로 예상되는 도전 횟수는 다음과 같습니다.

평균적으로 최소 0.64번의 도전에 성공하거나, 평균적으로 최대 2.21번의 시도 끝에 성공할 확률이 높다는 의미입니다.

 

다만 1번의 성공을 위해서는 최소한 1번의 도전이 필요합니다. .

따라서, 해석시에 최소 0.64번의 도전으로 해석해서는 안됩니다.

 

이항분포는 확률분포이며, 여기서의 분산은 확률변수의 모양을 결정지어 주는 요소입니다.

그래프의 개형을 그릴 때 참고요소이며, 최종해석은 달라져야 합니다.

 

여기서의 최종 해석은 최소 1번의 도전에 성공하거나,

평균적으로 최대 2.21번 시도시 성공할 확률이 높다는 의미입니다.

 

기하분포 해석시 또 다른 주의사항은 기하분포의 가정에 관해서 입니다. 

기하분포는 앞서의 성공여부, 실패여부는 영향을 미치지 않는다고 가정합니다.

즉, 실패를 많이 했다고 해서, 이후의 성공의 가능성을 낮추지는 않는다고 가정하므로, 

기존의 실패로 인해 향후 성공가능성에 영향을 주는 경우에는 예측확률과 어긋날 가능성이 높습니다.