[python/파이썬] 이항분포

변수는 랜덤하게 발생하거나, 일정한 확률을 가지고 발생합니다.

일정한 확률을 바탕으로 발생하는 변수를 확률변수(Random Variable)라고 합니다.

 

확률변수들이 모여 확률분포를 이루게 됩니다.

 

데이터의 확률분포를 알고 있다면, 

일어날 수 있는 사건의 확률을 알 수 있고, 확률에 근거한 판단을 내릴 수 있습니다. 

 

확률분포는 주사위처럼 결괏값이 떨어져 있는 이산형 확률분포와

키와 몸무게와 같이 연속적으로 변하는 값들로 이뤄진 연속형 확률분포가 있습니다.

 

이산형 확률분포에는

베르누이 시행, 이항분포, 포아송분포, 기하분포, 음이항분포, 초기하분포 등이 있습니다.

 

연속형 확률분포에는

균등분포,  정규분포, 표준정규분포, 지수분포, 감마분포, 카이제곱분포, F분포, t분포 등이 있습니다.

 

 

이항분포(Binomial Distribution)

결괏값이 성공과 실패, 합격과 불합격, 앞면과 뒷면 등과 같이,

단 두 가지의 가능성만 있을 때 이를 베르누이 시행이라고 합니다. 

베르누이 시행은 한 번의 시행을 전제로 하며, 

이항분포는 여러번 시행을 전제로 합니다. 

 

연구 결과, 어떤 사건이 성공할 확률은 0.7 즉 70%라고 가정하겠습니다.

따라서 실패할 확률은 1에서 성공할 확률 0.7을 뺀 0.3이며, 30%입니다. 

이 사건이 한 번 발생하면 베르누이 시행과 동일하며,

이 사건이 세 번 발생했을 때 이항분포의 확률을 구해보겠습니다. 

 

모든 경우의 수는 8가지입니다. 

매번 두 가지의 가능성이 있어서, 2배씩 늘어나므로 2 x 2 x 2 = 8이 됩니다. 

 

모든 경우의 수입니다.

모두 실패한 경우 = 실패, 실패, 실패

한번 성공한 경우 = 성공, 실패, 실패 // 실패, 성공, 실패 // 실패, 실패, 성공

두 번 성공한 경우 = 성공, 성공, 실패 // 성공, 실패, 성공 // 실패, 성공, 성공

세 번 성공한 경우 = 성공, 성공, 성공

모두 실패한 경우의 확률은 실패할 확률 x 실패할 확률 x 실패할 확률입니다.

곱해주는 이유는 다음과 같습니다. 

 

주사위를 예로 들어 설명하면,

주사위를 던져서 1이 나올 확률은 1/6입니다. 

다시 주사위를 던져서 1이 나올 확률은 1/6입니다.

첫번째 주사위가 1이 나왔다고 해서, 두번째 주사위가 1이 나오지는 않습니다. 

 

또한 첫번째 주사위는 1, 2, 3, 4, 5, 6 중 하나만 나오고, 

첫번째 주사위가 1이 나온 경우에, 두번째 주사위는 1, 2, 3, 4, 5, 6 중 하나가 나옵니다. 

첫번째 주사위가 2가 나온 경우에, 두번째 주사위는 1, 2, 3, 4, 5, 6 중 하나가 나옵니다.

첫번째 주사위가 3, 4, 5, 6이 나온 경우에도 각각 6가지 경우의 수가 있습니다. 

따라서 모든 경우의 수는 6과 6을 곱하여 36가지가 됩니다. 

 

이중 첫번째와 두번째 모두 1이 나오는 경우의 수는,

첫번째 주사위가 1이 나오고, 두번째 주사위도 1이 나오는 경우이며, 한 가지밖에 없습니다. 

 

그래서 첫번째와 두번째 모두 1이 나오는 확률은 해당 경우의 수(1) / 전체경우의 수(36)가 되어 1/36이 되며,

이는 첫번째 주사위가 1이 나올 확률 1/6과 두번째 주사위가 1이 나올 확률 1/6을 곱한 것과 같습니다. 

 

즉 모두 실패한 경우의 확률은 첫번째 실패할 확률 x 두번째 실패할 확률 x 세번째 실패할 확률입니다.

실패할 확률은 0.3이므로, 0.3 x 0.3 x 0.3이 되어 0.027이 되며, 2.7%가 됩니다. 

여기서 괄호의 3과 0의 의미는 세번의 시도 중 성공한 적이 없는 경우의 수이며, 

첫번째 실패, 두번째도 실패, 세번째도 실패한 경우만 해당되어 한가지 경우의 수밖에 없습니다.

math의 comb 메서드를 활용하며, 첫번째 인자는 도전 횟수, 두번째 인자는 성공 횟수입니다.

여기서 comb는 combination의 줄임말이며, 이러한 계산을 뜻하는 조합의 영단어입니다.

 

한번 성공한 경우는 3가지 경우이며, 

첫번째 성공, 두번째 실패, 세번째 실패하거나(0.7 x 0.3 x 0.3 = 0.063),

첫번째 실패, 두번째 성공, 세번째 실패하거나(0.3 x 0.7 x 0.3 = 0.063),

첫번째 실패, 두번째 실패, 세번째 성공(0.3 x 0.3 x 0.7 = 0.063)하는 경우입니다.

이 모든 경우의 확률을 더하면 0.063 + 0.063 + 0.063은 0.189가 되어 18.9%가 됩니다.

여기서 괄호의 3과 1의 의미는 세번의 시도 중 성공한 적이 한 번인 경우의 수이며,

한 번 성공한 경우의 수는 성공, 실패, 실패 // 실패, 성공, 실패 // 실패, 실패, 성공의 경우로 총 세 가지가 있습니다.

 

여기서 각각의 확률은 모두 확률을 곱하지만, 각각의 경우의 확률은 모두 더하였습니다. 

더해주는 이유는 다음과 같습니다. 

 

주사위를 예로 들어 설명하면,

첫번째 주사위를 던져서 1이 나올 확률은 1/6입니다. 

첫번째 주사위를 던져서 2가 나올 확률은 1/6입니다.

주사위를 한번 던질 때 1과 2는 동시에 나올 수 없습니다. 

그래서 주사위가 1 또는 2가 나올 확률은 각각의 확률을 더하여 2/6이 됩니다.

 

두 번 성공한 경우도 3가지 경우이며, 

첫번째 성공, 두번째 성공, 세번째 실패하거나(0.7 x 0.7 x 0.3 = 0.147),

첫번째 성공, 두번째 실패, 세번째 성공하거나(0.7 x 0.3 x 0.7 = 0.147),

첫번째 실패, 두번째 성공, 세번째 성공(0.3 x 0.7 x 0.7 = 0.147)하는 경우입니다.

이 모든 경우의 확률을 더하면 0.147 + 0.147 + 0.147은 0.441가 되어 44.1%가 됩니다.

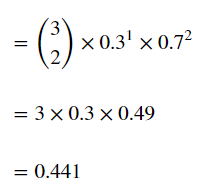
세 번 모두 성공한 경우는 1가지 경우입니다.

첫번째 성공, 두번째 성공, 세번째 성공(0.7 x 0.7 x 0.7 = 0.343)하는 경우입니다. 

그래서 모두 성공한 경우의 확률은 0.343이 되어 34.3%입니다. 

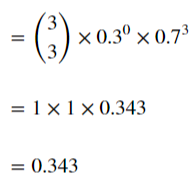
구해진 모든 확률을 더하면, 2.7% + 18.9% + 44.1% + 34.3%가 되어 100%가 됩니다.

 

여기서 2.7%, 18.9%, 44.1%,  34.3%의 분포가 바로 이항분포입니다.

 

이항분포는 이산형 확률분포이며,

이산형 확률분포의 기댓값은 각각의 기대되는 값과 이에 해당하는 확률을 곱한 후, 모두 합한 값입니다.

 

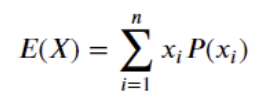
이를 이항분포에 적용하겠습니다. 

성공은 1, 실패는 0으로 합니다. 

기댓값 수식에 대입한 결과입니다.

첫번째 성공 1과 성공할 확률 0.7을 곱하면 0.7입니다.

두번째 성공 1과 성공할 확률 0.7을 곱하면 0.7입니다.

세번째 성공 1과 성공할 확률 0.7을 곱하면 0.7입니다.

이를 모두 더하면 2.1입니다.

파이썬 내부에서 취급하는 수의 자릿수가 한정되어, 아래와 같이 표시되나,

실제 결괏값은 세 성공확률의 합은 2.1이 됩니다.

사실 위의 세 식은 동일합니다. 

'첫번째 성공 여부는 두번째와 세번째 성공 여부에 영향을 미치지 않는다'라고 전제하였기 때문입니다.

통계학에서는 이러한 경우를 사건의 독립이라고 합니다.

따라서 매번 시행할 때마다 새롭게 시행하는 것과 같으며,  그 결과 세 식은 동일합니다.

 

결국 이항분포의 기댓값은 시행 횟수 x 확률입니다.

성공확률이 70%(0.7)이고, 실패확률이 30%(0.3)인 상황에서, 

세 번을 도전하면, 2.1번의 성공을 기대할 수 있다는 의미입니다.

 

수식을 이해하기 위해 직접 계산하여 기댓값을 구하였으나,

scipy의 binom.expect를 이용하여 이항분포의 기댓값을 간단히 구할 수 있습니다.

binom은 이항분포를 뜻하는 binomial의 줄임말이며, 

expect는 기댓값을 뜻하는 expected values의 줄임말입니다.

인자로 들어가는 args의 첫번째는 시행 횟수이며, 두번째는 성공확률을 입력합니다.

 

이산형 확률분포의 분산은 각각의 편차를 제곱하고, 각각에 해당하는 확률을 곱한  후, 모두 더한 값입니다.

 

이를 이항분포에 적용하겠습니다.

 

우리가 구한 기댓값(expected_value)은 세 번의 시행에 대한 기댓값이므로,

이항분포의 분산을 구하는 식에서 입력되는 기댓값은 앞서 구한 기댓값을 시행 횟수로 나눠줘야 합니다.

즉 세번 도전의 결과, 성공에 대한 기댓값이 2.1(expected_value)이므로,

각각 도전에 대한 기댓값은, 세 번 도전에 대한 기댓값인 2.1(expected_value)을 3으로 나눈 0.7입니다. 

파이썬은 어느 것이 성공에 대한 기댓값인지 알지 못합니다. 

0은 실패, 1은 성공이라는 기준은 우리가 정한 기준이며,

파이썬은 0에 대해서도, 1에 대해서도 값을 구합니다. 

따라서 0과 1의 모든 경우를 포함해야 하므로 0일 때의 값과 1일 때의 값을 더합니다.

이는 이항분포의 분산을 구하는 식에서 첫번째 시행에 대한 값입니다. 

두번째 시행도, 세번째 시행도 값은 동일합니다. 

첫번째 시행이 두번째 시행에 영향을 미치지 않으며, 

두번째 시행도 세번째 영향을 미치지 않는 독립된 사건들이기 때문입니다. 

 

따라서 분산은 다음과 같습니다. 

수식을 이해하기 위해 직접 계산하여 분산을 구하였으나,

scipy의 binom.var를 이용하여 이항분포의 분산을 간단히 구할 수 있습니다.

첫번째 인자는 시행 횟수이며, 두번째 인자는 성공확률입니다. 

 

만약 이항분포의 시행횟수가 상당히 크고,

성공확률이 0에 가까운 경우에는 포아송분포에 가까워집니다. 

 

이항분포는 시행횟수와 성공확률을 곱한 값이 5를 초과하고,

시행횟수와 실패확률을 곱한 값도 5를 초과하는 경우는

정규분포에 가까워진다고 알려져 있습니다. 

 

본문의 예제와 같이 성공확률이 0.7이고, 실패확률이 0.3인 경우에는

17번의 시행부터 정규분포에 가까워집니다. 

 

만약 성공확률이 0.5이고, 실패확률이 0.5라면,

11번의 시행부터 정규분포에 가까워 집니다. 

다만 일반적으로는 30번 이상의 시행에 한하여 정규분포로 근사하여 계산합니다.