[python/파이썬] 산포도로서 사분위편차계수

데이터의 대푯값은 데이터를 하나의 특정수로 표현할 수 있다는 점에서 유용합니다.

다만 대푯값만으로 데이터를 접근하기에는 부족합니다. 

 

예를 들어 데이터가 평균 주위에 몰려있는 경우라면, 

평균을 대푯값으로 정하여 데이터를 파악할 수 있습니다. 

그러나 데이터 평균 주위에는 데이터가 없고, 

단순히 최댓값과 최솟값 주위에 데이터가 몰려있고,

이 값들을 단순 평균하여 나온 평균은 그 데이터를 대표한다고 보기 어렵습니다. 

 

그래서 산포도를 활용합니다. 

산포도란 개별 관측값들이 대푯값으로부터 흩어진 정도를 보여주며,

대푯값만으로는 부족한 데이터를 보다 잘 이해할 수 있도록 돕습니다. 

 

산포도에는 범위, 사분위범위, 평균편차, 사분편차, 분산, 표준편차 등이 있습니다. 

 

산포도를 통해 서로 다른 데이터들을 비교하는 경우, 

단위나 기준이 다르면 비교하기 어렵습니다. 

 

이때 상대적인 산포도인 사분위편차계수, 평균편차계수, 변동계수 등을 활용합니다. 

상대적 산포도는 모두 중앙값이나 평균으로 나누어 계수를 구하며,

이를 통해 단위나 기준을 상쇄하므로, 비교가 용이합니다.

 

 

사분위편차계수(CQD ; Coefficient of Quartile Deviation)

사분위편차계수는 사분편차를 중위수로 나누어 구합니다. 

 

사분편차는 제3사분위수에서 제1사분위수를 뺀 값을 2로 나누어서 구합니다.

 

사분위수는 데이터를 줄을 세우고, 4 등분하여 구합니다.

100명이 줄을 서있으면, 25번째 사람이 1사분위이며, 

50번째 사람이 2사분위이며, 75번째 사람이 3사분위입니다.

 

사분위수들은 numpy의 quantile 함수를 사용하며,

1사분위수는 인수를 0.25 입력하며 구합니다. 

같은 방식으로 2사분위수는 0.50, 3사분위수는 0.75입니다.

 

 사분편차는 제3사분위수에서 제1사분위수를 뺀 값에 2를 나므로, 다음과 같습니다.

중위수는 데이터를 가장 작은 값부터 순서대로 가장 큰 값까지 줄을 세운 후,

줄의 가운데 위치하는 값을 의미합니다.

 

중위수는 계산을 통하지 않고, 데이터의 위치에 기반하여 사용하는 대푯값입니다.

사분위편차계수는 중위수와 마찬가지로 위치에 기반하는 계수로서,

평균이 아닌 중위수로 나누게 됩니다.

 

중위수는 numpy의 median을 활용하며, 다음과 같습니다.

사분위편차계수를 구해 사분편차를 중앙값으로 나눕니다.

 

사분위편차계수는 두 개 이상의 데이터들의 상대적인 산포도를 비교하기 위해 사용합니다. 

이를 위해 위의 data와 평균 및 중위수가 동일한 데이터를 생성한 후,

사분위편차계수를 구하면 다음과 같습니다. 

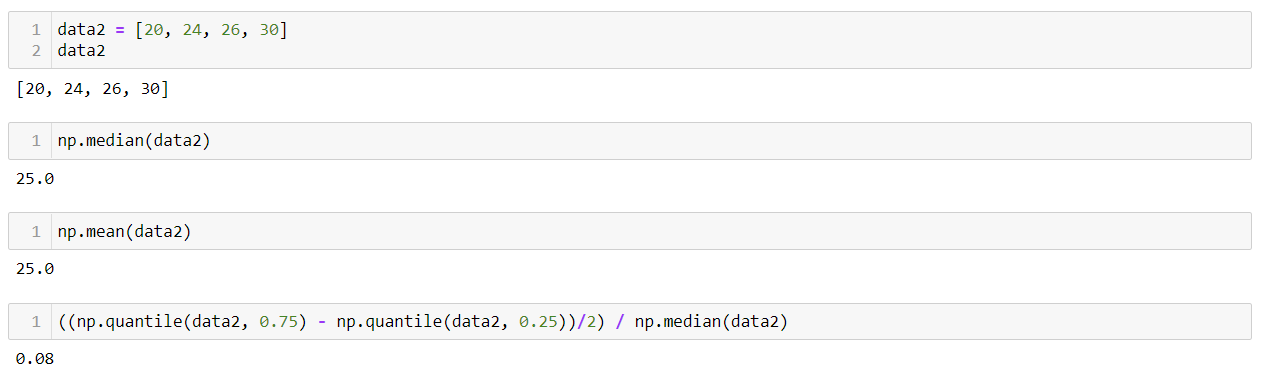
data에 비해 산포도가 적은 data2의 사분위편차계수를 비교하면, 

data의 사분위편차계수는 0.3이며, data2의 사분위편차계수는 0.08이므로,

data2의 산포도 정도를 수치로서 명확하게 비교할 수 있습니다.